filmov
tv
A Polynomial Ring R[x] is commutative iff R is Commutative - Proof- Euclidean Domain - Lesson 14

Показать описание
Download notes from Here:
Here in this video i will explain a theorem which states that A Polynomial Ring R[x] is commutative iff R is Commutative , which comes under the topic Euclidean Domain.
everything is explained in Hindi
welcome you all in my channel LEARN MATH EASILY
This video will be very useful if you are student of Higher Classes in mathematics like B.Sc, M.Sc , Engineering and if you are preparing for UGC Net and iit Jam etc.
Please Do not forget to Like, Share and Subscribe
Before this topic i did various other topics of Real Analysis:
My other Videos are as follows:
Metric Space
Countable and Uncountable Sets
Supremum & Infimum
Connectedness - Real Analysis
Compactness
Neighbourhoods and Limit Points- Real Analysis
Infinite Sequences - Real analysis
Indeterminate forms and l’hospital’s rule
Multiplication Tables- Shortcut tricks
Shortcut tricks to Solve linear equations
Quadratic Equations
Square and Cube Shortcuts
Number System
HCF And LCM
Multiplication Tricks
Subscribe to My YouTube Channel " Learn Math Easily" :
.................................................
My Page on Facebook:
.......................................................
Here in this video i will explain a theorem which states that A Polynomial Ring R[x] is commutative iff R is Commutative , which comes under the topic Euclidean Domain.
everything is explained in Hindi
welcome you all in my channel LEARN MATH EASILY
This video will be very useful if you are student of Higher Classes in mathematics like B.Sc, M.Sc , Engineering and if you are preparing for UGC Net and iit Jam etc.
Please Do not forget to Like, Share and Subscribe
Before this topic i did various other topics of Real Analysis:
My other Videos are as follows:
Metric Space
Countable and Uncountable Sets
Supremum & Infimum
Connectedness - Real Analysis
Compactness
Neighbourhoods and Limit Points- Real Analysis
Infinite Sequences - Real analysis
Indeterminate forms and l’hospital’s rule
Multiplication Tables- Shortcut tricks
Shortcut tricks to Solve linear equations
Quadratic Equations
Square and Cube Shortcuts
Number System
HCF And LCM
Multiplication Tricks
Subscribe to My YouTube Channel " Learn Math Easily" :
.................................................
My Page on Facebook:
.......................................................
Комментарии
![What is R[x]?](https://i.ytimg.com/vi/3vECJfVuI00/hqdefault.jpg) 0:05:09
0:05:09
 0:22:07
0:22:07
 0:08:47
0:08:47
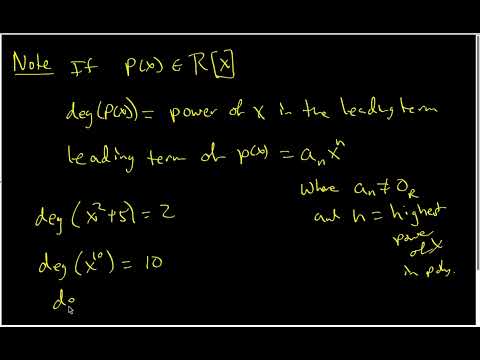 0:09:40
0:09:40
 0:05:56
0:05:56
 0:08:25
0:08:25
 0:08:22
0:08:22
 0:11:57
0:11:57
 0:20:58
0:20:58
 1:22:26
1:22:26
 0:05:22
0:05:22
 0:20:58
0:20:58
 0:11:57
0:11:57
 0:25:43
0:25:43
 0:01:54
0:01:54
 0:23:23
0:23:23
 0:52:47
0:52:47
 0:10:03
0:10:03
 0:15:42
0:15:42
 0:05:08
0:05:08
 0:16:51
0:16:51
 0:20:13
0:20:13
 0:45:38
0:45:38
 0:07:14
0:07:14