Abstract Algebra | If D is a UFD then D[x] is a UFD.

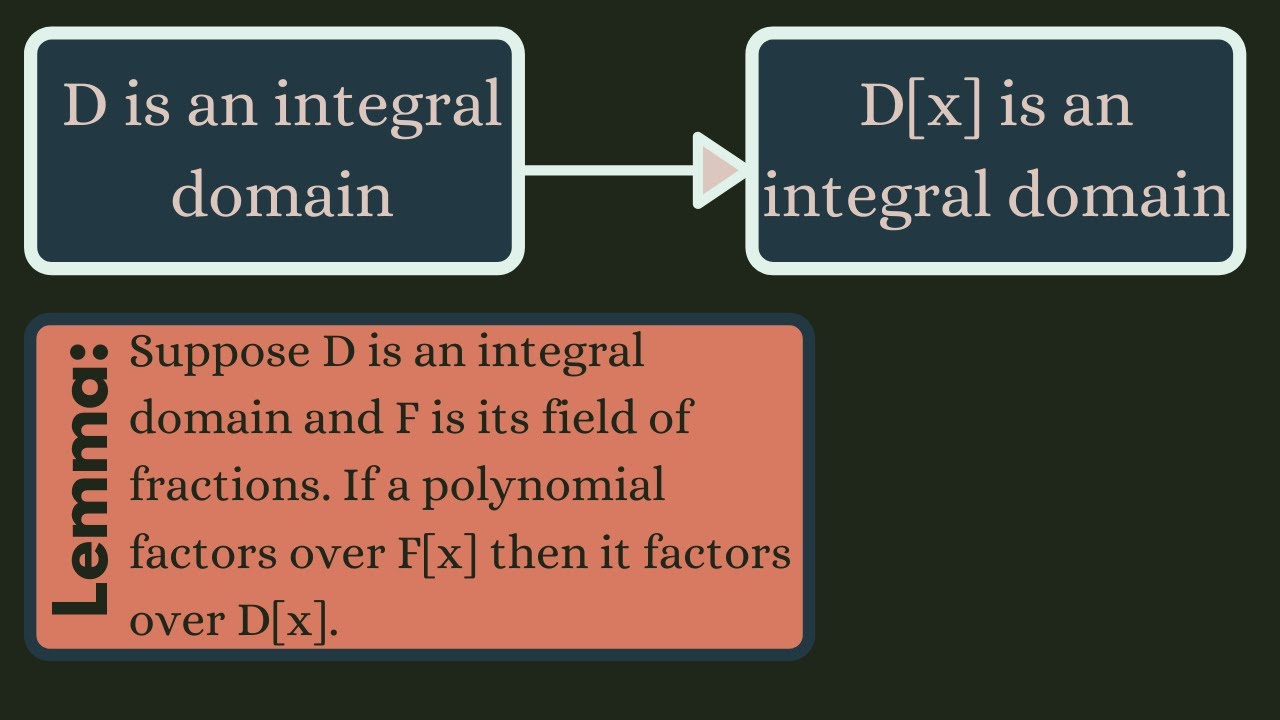
We prove an important result that states the ring of polynomials whose coefficients are from a unique factorization domain is itself a unique factorization domain. Along the way, we define the content of a polynomial, prove Gauss' lemma, and prove that if a polynomial factors over the field of fractions of an integral domain, then it also factors over the integral domain itself.

[DarkMonolth]

Loving these abstract algebra videos. It's easily my favorite subject in higher math

[thehappyapy]

My God. I had forgotten how much I loved higher algebra. I'm so rusty it's embarrassing, but this was very enjoyable to watch.

[ikramefa]

Hi for the exercice Olympide Romania. P a prime a0=p and an+1 = 2 an _ 1. We can find easialy an . If we considere vn = an -1 . Vn is a geometric sequence with 2 ‘ raison’ and p-1 first terme so vn = 2^n *( p-1) then an = 2^n *(p-1) +1 and then everyting will be easy

[rupaliyadav]

Can anyone plzz explain what is content of a primitive polynomial

[MsSlash]

Thank you! Could you please make a video about Hopf Algebras? I’ve noticed that Youtube lacks videos about it, except for lectures and daunting conferences.

[randomtiling]

Great video as always! I'm curious if you're ever planning on doing a video giving an introduction to some of the ideas in your research. The definition of VOAs seems pretty daunting, so it'd be interesting to see how you'd approach it.

[s.chitratta]

Doesn’t the second Lemma imply Gauss’ Lemma?

[bttfish]

I wish you can make some videos on combinatorial problems

[maxamedmuuse]

sir can you please help me out solve 2^x+3^y=72
2^y+3^y=108