Volume of Solids of Revolution | Cartesian & Parametric Form BY GP Sir

📒⏩Comment Below If This Video Helped You 💯
Like 👍 & Share With Your Classmates - ALL THE BEST 🔥

This video lecture " Volume of Solid of Revolution will help Engineering and Basic Science students to understand following topic of of Mathematics:
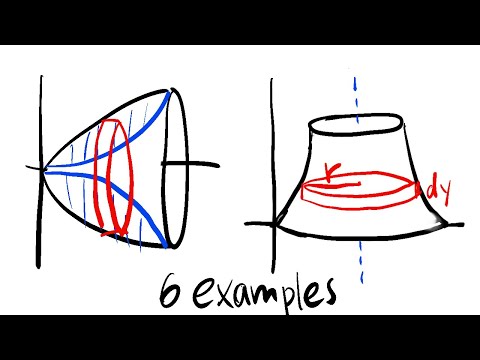
1. What is Volume Solids when it is revolve about X-axis & Y-axis
2. Working rule For Finding Volume of Solid of Revolution (Cartesian & Parametric Form)
3. What is volume of Sphere/Loop/Astroid When it is revolve about axis.
4. This is part of Integral Calculus
#VolumeOfSolids #Revolution #IntegralCalculus #GATE #JAM
This Concept is very important in Engineering & Basic Science Students. This video is very useful for B.Sc./B.Tech students also preparing NET, GATE and JAM Aspirants.
Find Online Engineering Math 2018 Online Solutions Of Volume of Solids of RevolutionCartesian & Parametric Form BY GP Sir Gajendra Purohit.
Do Like & Share this Video with your Friends. If you are watching for the first time then Subscribe to our Channel and stay updated for more videos around Mathematics.

Time Stamp
An introduction - 0:00
Formula of Volume of solid of Revolution - 1:13
Example 1 - 1:39
Example 2 - 3:57
Example 3 - 7:38
Example 4 - 10:08
Example 5 - 13:26
Conclusion of video - 17:21
Detailed about old videos - 17:43

📚 Our Book Publications

🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹🔸🔹

👤 My Social Media Handles


✅Our YouTube Channels

📚 Important Course Playlists

📚 Following Topics Are Also Available

📷 My Equipment & Gear

Thanks For Watching My Video 🙏🏻
Like, Share & Subscribe 💯
Dr.Gajendra Purohit

[gajendrapurohit]

Thanks for your comment, your appreciation always motivate us to do such kind work.






Keep Watching OUR latest video.







Following Topics are also Available
















Please share it with your Friends

Thanks

Dr.Gajendra Purohit

[rajarammishra]

Semester is over our head and GE maths syllabus is not complete yet. Thank god your videos are there sir. Otherwise our brains might have gone roasted.

[amayrasharmasharma]

Sir seriously it's really very nice.. Thks u Sir

[gajendrapurohit]

Thanks for your comment, your appreciation always motivate us to do such kind work.
Keep Watching OUR latest video.
Topic:- Asymptotes
Topic:- Laplace Transform
Topic:- Vector Calculus
Topic:- Partial Differential Equation
Topic:- Second Order Differential Equation with Variable
Topic:- Higher Order Differential Equation With Constant Coefficient
Topic:- Differential Equation (First Order & Degree)
Topic:- Fourier Series
Topic:- Matrices
Topic:-Fourier Transform
Topic:-Curve Tracing
Topic:-Volume of Solids of Revolution
Please share it with your Friends
Thanks
Dr.Gajendra Purohit

[MdSajid-dihk]

Sir your attitude is normal but your knowledge is huge. And the way you teach is very simple and easy and interesting... Keep teach us... Now math will be interesting for everyone. If you agree with this comment.. Like here. For sir.

[p_ghosh]

Sir, you are the reason I'm passing my math exams.

[RajeshRanjan-esnk]

Sir I am very thankful to you because your teachings helped me a lot... the content delivery is very good... the examples you take are up to the mark and the way of teaching is fabulous. You are a very good teacher.

[sanjaykr.m]

Sabse bari bat h ki work fast hota h jo ki pata nhi chalta, pressure kabhi nhi feel kiye . etna kam time me kafi contain de dete h. its just like miracles. Pranam pujniye GURUJI.

[adityanarayanm]

i am in NIT and sir you teach better than my college professors....

[ramnareshyadav]

Nice lecture but when you have time than vector space .Dynamic and Statistics lecture also.

[gauravsaini]

Sir i always see all videos and your videos is very important for all student 😍

[gkgsdotcom]

बहुत अच्छे से समझ में आ रहा है upload more and more video lecture

[durgaraonaram]

Hello sir...I go through your classes, I like your explanation. I request to to give a solution for this problem...." The volume generated by revolving the curve y^4=x(4-x) along x-axis "

[pranjitborah]

Sir o to π/2 ingregation of sin^nx cos^nx we can use walles formula
Which is easy to find answer
Am i right 🥰

[nidhiupadhyay]

Sirrr u're teaching style is great 🙏🙏🙏

[andromedagalaxy]

I like math, and after watching your videos I become a fan of you Sir.. really interesting..I appreciate it 👍👍

[ankitsaini]

Find the volume of the solid generated by revolving the region bounded by 𝑦=√𝑥 and the lines 𝑦=1, 𝑥=4 about the line 𝑦=1.

[karanrawat]

You are doing such a noble work sir, thank you...

[br__panditji]

You are also a great teacher in my life 🙂🙂❣️❣️.

[sanjaykr.m]

Sir, PLZ....ap se request h ki important theory ka lecturer daliye, jo exam point of view se ho. Mujhe bahut behatarin lagta h ap ka class. Thank you sir