filmov
tv
1-1+1-1+1-1+1...? #shorts

Показать описание
This series goes on forever. Sometimes it's 1. Sometimes it's 0. Can it ever be 1/2? Can we even know? WHAT IS THE ANSWER? #shorts
1-1+1-1+1-1+1...? #shorts
1,2,3 or 4?😀 #shorts
Flo Wirtz Kartoffel Ranking Teil 1 #shorts
One Two Buckle My Shoe by Edmondx & Blanco y Sancho #shorts
1 Millionen Abonnenten🙏🏽❤️ | Lewinray #shorts
1 MANGO OR TV? #shorts
2 Wahrheiten, 1 Lüge😰Freunde sind geschockt😱AlpaySanti #Shorts
(SUKI SUKI DAISUKI)Who'stheBest?1,2,3 or 4?#shorts #tiktok #viral
Musikvideo nachstellen Part 1 #shorts
1 = -1 #shorts
1 Ipad or 1 Cherry? - #shorts
🗣 Mashup 68+1 featuring Danielle Threet (TikTok), #shorts
Wie findet ihr die Nägel von 1-10?💅🏽 #shorts
Inside Out Finger Heart 🫶🏻 PART 1 #shorts
Japanese Method #shorts
Words per Year | Part 1 #shorts
Rubik's Cubes From Level 1 to 100 (Part 2) #shorts
Er spielt 1 zu 1 wie RONALDO! 😳⚽️🐐 #shorts #jannikfreestyle
Noch 2k Abos dann sind wir 1,1mio 😳 #shorts
Rubik's Cubes From Level 1 to 100 #shorts
Talking Tom Shorts 1 - Red Alert
Paying 5,000 for 1 minute Rickshaw ride 😍 ytshorts #shorts
Rubik’s Cubes From Level 1 to 100 (Part 3) #shorts
1 like = 1 lépés! 😂 #shorts
Комментарии
 0:00:38
0:00:38
 0:00:15
0:00:15
 0:00:37
0:00:37
 0:00:10
0:00:10
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:00:59
0:00:59
 0:00:11
0:00:11
 0:00:17
0:00:17
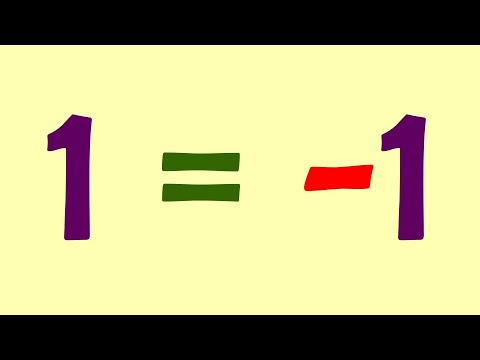 0:00:23
0:00:23
 0:00:29
0:00:29
 0:00:15
0:00:15
 0:01:01
0:01:01
 0:00:31
0:00:31
 0:00:20
0:00:20
 0:00:55
0:00:55
 0:01:00
0:01:00
 0:00:31
0:00:31
 0:00:31
0:00:31
 0:01:00
0:01:00
 0:00:50
0:00:50
 0:00:23
0:00:23
 0:01:00
0:01:00
 0:00:27
0:00:27