filmov
tv
Abstract Alg, Lec 34B: More Splitting Field Examples, Algebraic vs. Transcendental Field Extensions

Показать описание
Abstract Algebra, Lecture 34B. Field Theory and Galois Theory, Part 5.
(0:00) Encouragement to rewatch the lecture.
(0:22) Back to the example from the end of lecture 34A. Find a splitting field of x^4 + 1 over Q and find a splitting field of x^4 + 1 over R (the answers are different).
(2:11) Dimensions of these splitting fields as vector spaces over the base fields are different. This reflects the fact that x^4 +1 is irreducible over the rationals Q but reducible over the reals R (check that its reducible over R with Mathematica).
(8:55) Splitting field for x^5 - 1 over Q. Its reducible over Q because it factors as (x - 1)(x^4 + x^3 + x^2 + x + 1), where this second factor, call it g(x), is a cyclotomic polynomial which can be proved to be irreducible over Q by Eisenstein's criterion (applied to g(x + 1)).
(12:52) Will come back to an example of a splitting field over a finite field in Lecture 35.
(13:24) Insight into our notation for extension rings and extension fields (relate to notation for rings of polynomials and to fields of rational functions (fields of quotients of polynomials)).
(22:09) Algebraic and transcendental numbers. Algebraic and transcendental extensions.
(24:55) "Almost all" real numbers are transcendental but it is difficult to prove numbers that we "suspect" to be transcendental actually are. The fact that pi is transcendental is historically important the the problem of "squaring the circle" (producing a "quadrature" of a circle...constructing, with straightedge and compass, a square of equal area to a given circle).
(27:43) Characterizing algebraic versus transcendental simple extensions (isomorphism classes).
(29:14) Finite extensions (extensions that are finite dimensional vector spaces over the base field) and relationship to algebraic extensions. The dimensions multiply in a tower of fields.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:30:33
0:30:33
 0:19:43
0:19:43
 0:33:51
0:33:51
 0:14:41
0:14:41
 0:05:54
0:05:54
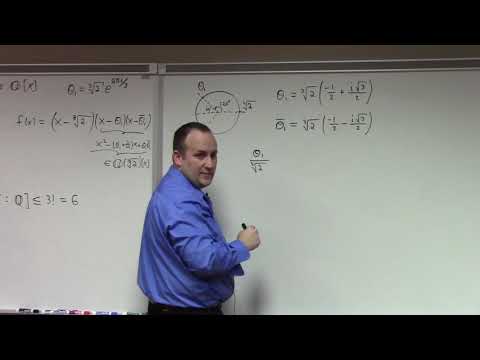 0:50:00
0:50:00
 0:34:46
0:34:46
 0:50:29
0:50:29
 0:08:25
0:08:25
 0:06:14
0:06:14
 0:34:03
0:34:03
 0:31:42
0:31:42
 0:02:51
0:02:51
 1:08:57
1:08:57
 0:48:41
0:48:41
 0:03:38
0:03:38
 0:52:10
0:52:10
 0:06:33
0:06:33
 0:08:41
0:08:41
 0:08:11
0:08:11
 0:52:13
0:52:13
 0:23:40
0:23:40
 0:19:51
0:19:51
 0:04:37
0:04:37