filmov
tv
Big O, Math, Logarithms, Heap, Binary Tree, and Computing Explained with Simple Live Example
Показать описание
This live demonstration shows:
1) A real life example of logarithms, applied to computing. This is great for mathematicians who are looking for a true example.
2) Said another way, an example of how math can be used to explain/demonstrate computing concepts.
I demonstrate the following concepts:
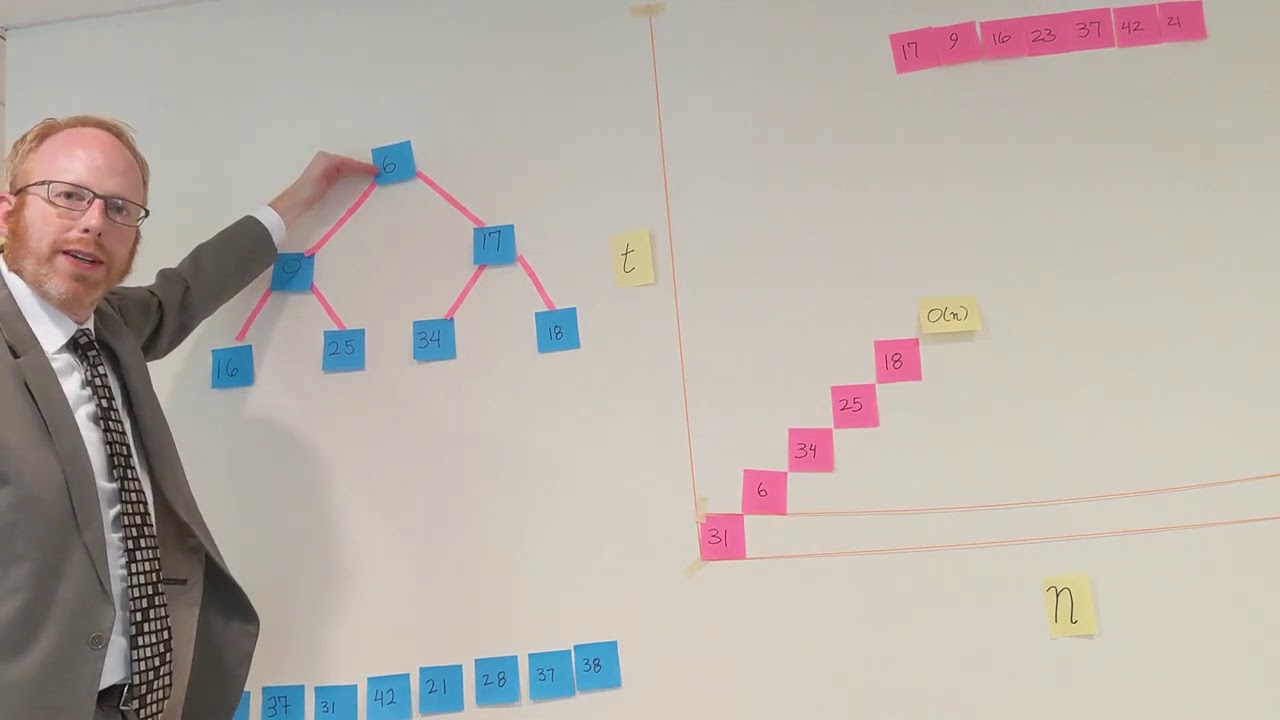
1) finding the smallest item in an array has O(n) performance.
2) inserting an item into an array has O(n) performance.
3) removing an item from an array has O(n) performance.
4) finding the smallest item in a binary tree has O(1) performance.
5) inserting an item into a binary tree has O(log-n) performance.
6) removing an item from a binary tree has O(log-n) performance.
Visualizing how logarithms worked helped me tremendously in college Calculus. This applied example includes a visualization, using a graph and some self-adhesive sticky notes. If you want to see a practical example of logarithms in real life, this video should help. If you're curious how important math is in computing, this video demonstrates one way it is.
Big-O notation is a study of algorithm performance as the units its operating on grows. Ideally, the algorithm should take no more time, even as the collection it is operating on grows. This is O(1). O(n) indicates that each new item to process equals one additional unit of time. We can slow this growth by using recursion, which gives us a slower growth rate of O(log-n). Slowing growth rate is key for scalability, or fitting more processing on a fixed set of resources.
The binary tree/heap is one technique we can use to slow growth from O(n) to O(log-n). It uses recursion during inserting and removing an item. Seeing the lowest value on a min heap, or the highest value on a max heap, is an O(1) operation, because you simply have to look at the top of the heap. In this video, I show how that works through an example.
1) A real life example of logarithms, applied to computing. This is great for mathematicians who are looking for a true example.
2) Said another way, an example of how math can be used to explain/demonstrate computing concepts.
I demonstrate the following concepts:
1) finding the smallest item in an array has O(n) performance.
2) inserting an item into an array has O(n) performance.
3) removing an item from an array has O(n) performance.
4) finding the smallest item in a binary tree has O(1) performance.
5) inserting an item into a binary tree has O(log-n) performance.
6) removing an item from a binary tree has O(log-n) performance.
Visualizing how logarithms worked helped me tremendously in college Calculus. This applied example includes a visualization, using a graph and some self-adhesive sticky notes. If you want to see a practical example of logarithms in real life, this video should help. If you're curious how important math is in computing, this video demonstrates one way it is.
Big-O notation is a study of algorithm performance as the units its operating on grows. Ideally, the algorithm should take no more time, even as the collection it is operating on grows. This is O(1). O(n) indicates that each new item to process equals one additional unit of time. We can slow this growth by using recursion, which gives us a slower growth rate of O(log-n). Slowing growth rate is key for scalability, or fitting more processing on a fixed set of resources.
The binary tree/heap is one technique we can use to slow growth from O(n) to O(log-n). It uses recursion during inserting and removing an item. Seeing the lowest value on a min heap, or the highest value on a max heap, is an O(1) operation, because you simply have to look at the top of the heap. In this video, I show how that works through an example.
0:15:33
Big O, Math, Logarithms, Heap, Binary Tree, and Computing Explained with Simple Live Example
0:10:24
Deeply Understanding Logarithms In Time Complexities & Their Role In Computer Science
0:20:38
Big-O Notation - For Coding Interviews
0:06:25
Learn Big O notation in 6 minutes 📈
0:05:13
Big-O notation in 5 minutes
0:14:30
Proving log n is O(n) [Big-Oh Bootcamp]
0:15:32
Build Heap Algorithm | Proof of O(N) Time Complexity
0:08:55
11 BIG O of Binary Heaps
0:40:18
Investigating Heap Sort - Why Is Heap Sort Θ(n * log(n))? An Even Longer Really Long Answer.
0:10:48
What Big-O notation ACTUALLY tells you, and how I almost failed my Google Interview
0:15:46
1.8.1 Asymptotic Notations Big Oh - Omega - Theta #1
0:10:51
Top 6 Coding Interview Concepts (Data Structures & Algorithms)
0:23:16
Asymptotic Notations 101: Big O, Big Omega, & Theta (Asymptotic Analysis Bootcamp)
0:51:08
2.6.3 Heap - Heap Sort - Heapify - Priority Queues
0:36:22
Introduction to Big O Notation and Time Complexity (Data Structures & Algorithms #7)
0:18:36
CS3130SP2020HeapCost
0:08:50
CalcGREEN 1 : Ch. 10.4 : Big-O & Computational Complexity
0:05:50
15 Sorting Algorithms in 6 Minutes
0:20:31
Big O Notations
0:00:44
3 Tips I’ve learned after 2000 hours of Leetcode
0:05:30
Heap Insertion Running Time
0:12:40
Introduction to Big-O
0:00:34
Human Calculator Solves World’s Longest Math Problem #shorts
0:10:08
1.5.1 Time Complexity #1
Комментарии