Asymptotic Notations 101: Big O, Big Omega, & Theta (Asymptotic Analysis Bootcamp)

📹 Intuitive Video Explanations
🏃 Run Code As You Learn
💾 Save Progress
❓New Unseen Questions
🔎 Get All Solutions

Today we will initiate a discussion on something that I have lied to you about for a very long time. This will be as simple as possible.

We will not only consider the informal definition but rather also look at the mathematical understandings behind why we call these asymptotic “bounds”.

Again, we care about this because the true colors of an algorithm can only be seen in the asymptotic nature of runtime and space.

So imagine this, we have these components:

A function T(n) which is the actual number of comparisons, swaps...just...resources an algorithm needs in terms of time or space. It is a function of n. When n changes, T(n) changes.

Our job is to classify behaviour.

A bound O( f(n) ) is the function that we choose to apply for the specific bounding.

The definitions, an example:
"T(n) is O(f(n))" iff for some constants c and n0, T(n) less than or equal to c * f(n) for all n greater than or equal to n0

In English...this means...we can say that f(n) is a fundamental function that can upper bound T(n)'s value for all n going on forever.

We have an infinite choice for what c is.

Our constant does not change behavior, it changes "steepness" of the graph.

We are saying that...if I declare f(n) as an upper bound, then I can find a constant c to multiply against f(n) to ALWAYS always always keep T(n) beneath my c * f(n)...T(n) will never beat c * f(n) for infinite n values...hence asymptotic bounding.

If we can't find this c then f(n) fails as an upper bound because it does not satisfy the asymptotic requirement.

So why are constants dropped?

Well...think about what we just did. The injection of the arbitrary c as a multiple onto a base function removes the need for a constant. It adds no meaning to a bound because it is conceptually already a part of the definition of what a bound is.

Big Bounds

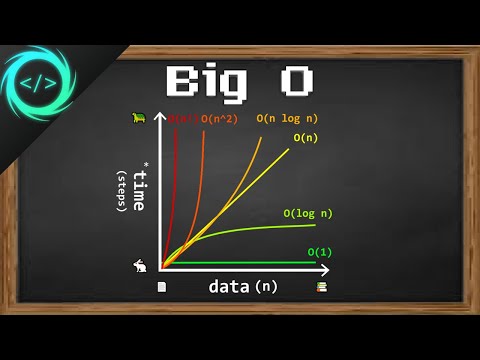
Big O: Upper bound on an algorithm's runtime

Theta (Θ): This is a "tight" or "exact" bound. It is a combination of Big

For example:
An algorithm taking Ω(n log n) takes at least n log n time, but has no upper limit.

An algorithm taking Θ(n log n) is far preferential since it takes at least n log n (Ω(n log n)) and no more than n log n (O(n log n)).

Big Omega (Ω): Lower bound on an algorithm's runtime.

Little Bounds

Little o: Upper bound on an algorithm's runtime but the asymptotic runtime cannot equal the upper bound.

There is no little theta (θ).

Little Omega (ω): Lower bound on an algorithm's runtime but the asymptotic runtime cannot equal the lower bound.

If you can't get an exact upper bound, try lower bounding (although it is less useful to be honest).

++++++++++++++++++++++++++++++++++++++++++++++++++

#asymptoticnotations

[LegacyCS]

I really appreciate how you said at the beginning "Do you understand this? Because I don't, this is too thick for me, but this is the typical introduction you'd get in actual classes". This whole sentence resonated so much with me. Sometimes I cannot grasp those abstract ideas in math, and I just need to have the concepts explained to me like im 5 years old, and your video was able to make me understand this in just 20 minutes, when I've been struggling with this for 3 years. Thank you man, keep it up!

[ful]

I had to pause the video to take the time to say this. Your videos are absolutely phenomenal. Keep up the good work man, your channel is 10x better than all the others I see that just tell you "how" to do something but don't go over the "why". Great stuff man, your channel will grow soon enough. Definitely recommending this channel to all my other friends.

[suparnobhattacharya]

The day this guy stops making videos we'll be doomed.

[BackToBackSWE]

This is Ben from 5 months in the future. Cool video man.

[hands]

This is my first comment I've ever written on YouTube that I can recall. There is no better opportunity than to give you feedback as my first post.

I want to personally applaud you, not just for your excellent teaching (you a BEAST!), but the effort you take to thoroughly respond to all of your subscribers. That speaks volumes. This is what stood out to me aside from your incredible ability to convey these complex topics in an understandable way. You won my subscription.

What sets you apart from many other channels is how humble you are. You don't proclaim to be born as Knuth's twin brother or anything like that. You shared with us how you personally struggled with the same concepts that we now are an audience to. This quality makes you tangible. It draws people closer to you: "Hey! He was once where I was. I'm not alone. I can overcome these obstacles like he did!".

On that note, keep up the remarkable work. You have a gift and people out there in cyberspace are watching.

[valentinascharpf]

I've been "kind of" getting these concepts for years, never quite being able to really get them. But I really understand now. Wow! I cannot believe it. Thank you!!! Some people are meant to be teachers. You are absolutely one of those. I agree with the others: you have a gift.

[abrantapia]

I rarely leave comments but thank you for explaining this like a normal person. I got overwhelmed with my textbook like it was purposely trying to prevent me from learning. You guys are phenomenal.

[diegocastro]

Hey man just wanted to thank you. Reviewing big O for my algorithms class and I am happy to say this is hands down the best explanation for this out there!

[nononono-lmid]

all I ask....please DONT ever stop making videos man...you are helping a lot of people with these vids

[rohitkarnati]

This man literally called me out haha, I was scrolling to look at the comments and got off task and he said "you still with me" 4:57 and I was like yes sir.

[suparnaprasad]

Absolutely amazing. Learnt more in 23 minutes than 1.5 hours of class. Looking forward to more such content!!

[brianperez]

This was legitimately the most helpful video I've ever seen. When my professor tried explaining this concept, it sounded like gibberish for 45 minutes. After watching this video, I completely understand the concept. Thank you so much for your help!

[af_]

I have paused at 15 minutes to say - thank you! This video helped me understand this topic very nicely.

I thought I was good at algorithms and data structures and time complexity stuff last year until they introduced this from a mathematical standpoint this year.

This really helped.

[alkendimacale]

omg wtf. I actually understood this holy shit. You're amazing dude, wish you were my prof hahahahha

[samanthasavoy]

I don't normally comment on youtube, but I had to say that you are a phenomenal teacher. Cannot thank you enough for how you explained this concept!!!

[slnaisld]

had to pause the video to say that the way you explain this is so refreshing. I thought it was going to be hard to understand but your explanation really helped. Thank you!!!

[nehagawhane]

Pausing at 8:33 where it magically starts making sense to me, you are amazing! I dont comment often but you deserve a wide reach and endless growth, thank you for doing this!

[saloni]

I'm writing this in the time of quarantine from my home and it's the first ever video I saw from your channel and I absolutely love this!!!!
I've been trying to figure out asymptotic notations since a long time and I finally got it for the first time ever.
TYSM for your hard work <3

[ihavenoname]

Never comment or like anyone YouTube but this dude KNOWS what he's talking. and thank to him, I got every single point he explained super clear!

[TheZombyKillr]

Thank you so much for explaining this. As a graduate student in my 5th year of CS, I have only had bad luck with professors. No one would ever use examples or simplistic breakdowns to explain the concept, as you did in this video. You state the problem, simplify it, solve it, and work back up to the complex level we started at, in a way that makes it easy to understand, and very easy to follow. My assignments finally seem clear to me now. You've earned a sub :) Have a good week!