filmov
tv
Can we find c that satisfies the conclusion of the mean value theorem? Calculus 1 tutorial

Показать описание
Can we find c that satisfies the conclusion of the mean value theorem? Calculus 1 tutorial
Can we find c that satisfies the conclusion of the mean value theorem? Calculus 1 tutorial
SHORTCUT - FIND C THAT MAKES F CONTINUOUS ON (-infinity, infinity)
Learn how to find the value c that completes the square
Find the value of c that completes the square
Find the value of c that makes the function a probability density function
FIND THE VALUE OF C THAT MAKES THE PIECEWISE FUNCTION CONTINUOUS EVERYWHERE
Can You Find The Value of C=? From Equation Involving Complex Number | Math Olympiad
Learn how to find the value c that creates a perfect square trinomial, x^2 - 7x + c
Find the value c that fills in the hole to make the function continuous
Find c guaranteed by the Mean Value Theorem for f(x) = x^7 over [0, 7]
Find C So That Function Is Continuous
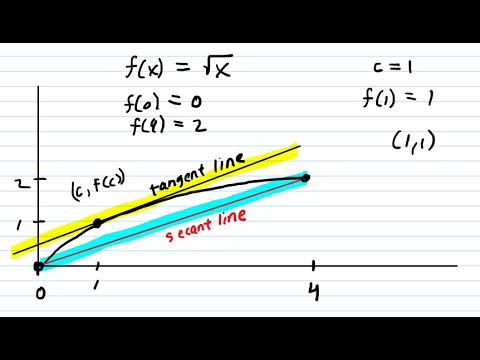
Find the number c that satisfies the conclusion of the mean value theorem
How to Find the Value of c in the Intermediate Value Theorem Quadratic Example
Find C to Create a Perfect Square Trinomial
Find all numbers c that satisfies the Mean Value Theorem f = x^3 -3x +2 on the interval [-2, 2]
Find the number c that satisfies the conclusion of the mean value theorem
Putnam Math Competition Question | Find c so two shaded areas are equal | Caiculus method
How to Find the Value of c in the Mean Value Theorem Example with f(x) = 7sin(x)
Complete the Square - Find c
Morningstar - No Place To Find ft The C (Official Music Video)
Can you find the Value of Angle C? | Fast & Easy Tutorial
Can you find the values of A, B, and C??
Find the value of c that makes the function continuous on R
Letter C | Find the Letter C | The Singing Walrus
Комментарии
 0:05:39
0:05:39
 0:04:26
0:04:26
 0:01:59
0:01:59
 0:02:01
0:02:01
 0:03:25
0:03:25
 0:04:38
0:04:38
 0:05:25
0:05:25
 0:01:45
0:01:45
 0:04:31
0:04:31
 0:03:22
0:03:22
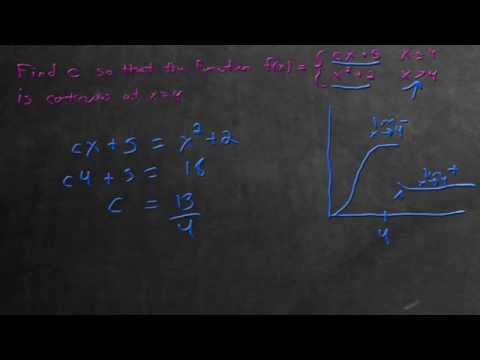 0:03:20
0:03:20
 0:06:55
0:06:55
 0:04:56
0:04:56
 0:03:27
0:03:27
 0:03:12
0:03:12
 0:07:27
0:07:27
 0:06:35
0:06:35
 0:04:05
0:04:05
 0:05:01
0:05:01
 0:03:14
0:03:14
 0:04:06
0:04:06
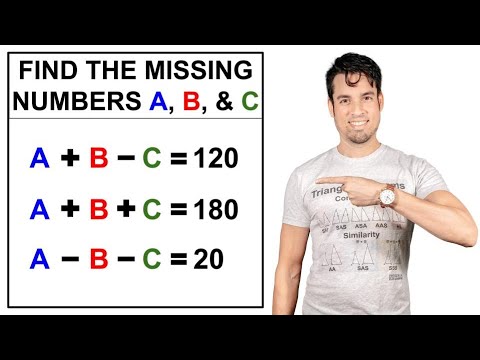 0:02:40
0:02:40
 0:05:39
0:05:39
 0:02:28
0:02:28