filmov
tv
Determine the form of a particular solution, second order linear differential equation, sect4.4 #29
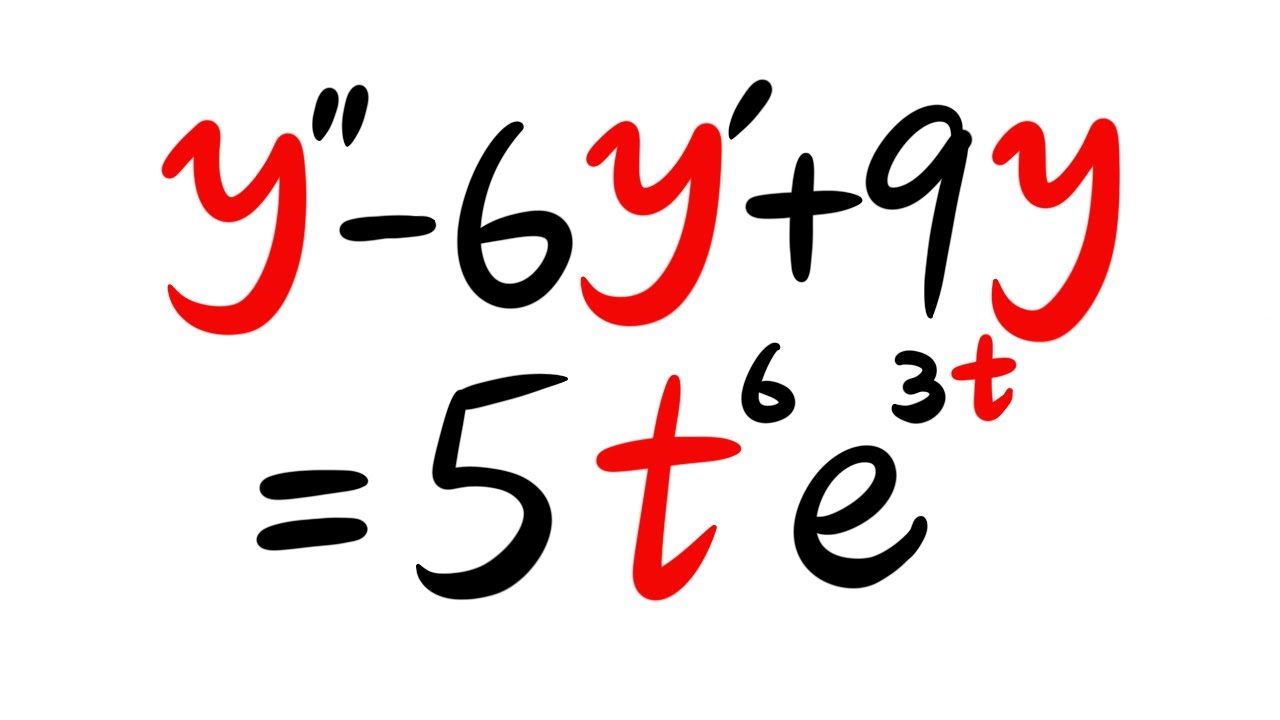
Показать описание
Form of a particular solution with undetermined coefficients,
particular solution for a non-homogeneous differential equation,
second order non-homogeneous linear differential equations,
For more calculus and differential equations tutorials, check out my new channel "just calculus":
To learn how to solve different types of differential equations:
#DifferentialEquations
particular solution for a non-homogeneous differential equation,
second order non-homogeneous linear differential equations,
For more calculus and differential equations tutorials, check out my new channel "just calculus":
To learn how to solve different types of differential equations:
#DifferentialEquations
Determine the form of a particular solution, sect 4.5#31
Determine the form of a particular solution, second order linear differential equation, sect4.4 #29
Determine the form of a particular solution, second order linear differential equation, sect 4.4 #27
Determine the form of a particular solution of the equation. u^''+2 u^'+10 u=2 …
Determine the form of a particular solution, second order linear differential equation, sect 4.4#31
How To Determine Which Pair of Ratios Forms a Proportion
Determine if solutions form a fundamental set
Determine the Equation of a Line in Slope-Intercept Form
Orange Poetry Film Festival 2024 || Happening Live
How to Determine the Form of the Rate Law | Professor Dave & Chegg Explain
Convert a vector to component form and determine the magnitude
Determine an Indefinite Integral in the Form: a*e^x-bcsc^2(x)
Determine Basic (Leading) Variables and Free Variables Given a Matrix in RREF
Determine the Equation of a Line Parallel to a Line in General Form
Determine the Magnitude of a Vector Given a Vector in Component Form (Ex 1)
How to Determine if Two Ratios Form a Proportion Using Simplifying | Math with Mr. J
Determine if each pair of Ratios forms a Proportion - Example
Determine Equation of Parabola From Graph in Standard Form
How to determine the general solution to a differential equation
Determine a particular solution to the given differential equation of the form y_p(x)=A_0 e^-3…
How To Determine The Discriminant of a Quadratic Equation
Determine the scale from a floor plan
How to Determine If an Ordered Pair is a Solution to a System of Equations
How to determine if three lengths form a triangle
Комментарии
 0:07:08
0:07:08
 0:04:21
0:04:21
 0:05:13
0:05:13
 0:00:33
0:00:33
 0:05:38
0:05:38
 0:01:28
0:01:28
 0:03:08
0:03:08
 0:08:25
0:08:25
 3:59:42
3:59:42
 0:04:21
0:04:21
 0:02:11
0:02:11
 0:03:34
0:03:34
 0:02:28
0:02:28
 0:03:42
0:03:42
 0:03:10
0:03:10
 0:04:57
0:04:57
 0:03:02
0:03:02
 0:03:56
0:03:56
 0:02:03
0:02:03
 0:00:33
0:00:33
 0:03:05
0:03:05
 0:04:09
0:04:09
 0:02:37
0:02:37
 0:01:48
0:01:48