filmov
tv
Parametrized Curves, Multivariable Calculus

Показать описание
Parametrizing curves in (x,y) and (x,y,z)-space with vector-valued functions r(t). As a curve is a one-dimensional object, it requires exactly one parameter "𝑡" for its complete description. We explore various examples of curve parametrization, including circles, line segments, and intersections of surfaces. (Unit 2 Lecture 3)
Key Points
1. Parameterization of Curves: Using a vector-valued function to describe a curve in a space.
2. One-Dimensional Nature of Curves: A curve, despite existing in a multi-dimensional space, is fundamentally one-dimensional.
3. Unit Circle Parameterization: Utilizing trigonometric functions to describe circles in different planes.
4. Line Segment Parameterization: A method to parametrize a straight line segment between two points.
5. Parabolic Curve Parameterization: Setting one variable as the parameter to describe a parabolic curve.
6. Intersection of Surfaces: Using a common variable as a parameter to describe the intersection of two surfaces.
#mathematics #math #vectorcalculus #multivariablecalculus #iitjammathematics #calculus3 #mathtutorial
Key Points
1. Parameterization of Curves: Using a vector-valued function to describe a curve in a space.
2. One-Dimensional Nature of Curves: A curve, despite existing in a multi-dimensional space, is fundamentally one-dimensional.
3. Unit Circle Parameterization: Utilizing trigonometric functions to describe circles in different planes.
4. Line Segment Parameterization: A method to parametrize a straight line segment between two points.
5. Parabolic Curve Parameterization: Setting one variable as the parameter to describe a parabolic curve.
6. Intersection of Surfaces: Using a common variable as a parameter to describe the intersection of two surfaces.
#mathematics #math #vectorcalculus #multivariablecalculus #iitjammathematics #calculus3 #mathtutorial
Parametric curves | Multivariable calculus | Khan Academy
Curves, Parameterizations, and the Arclength Parameterization
Parametrized Curves, Multivariable Calculus
How to Parametrize a Curve
Calculus 2 Lecture 10.2: Introduction to Parametric Equations
Sketching a Parametrized Curve
Multivariable Calculus - Lecture 1: Parametric Curves, and Calculus with Parametric Curves
Parametric Equations Introduction, Eliminating The Paremeter t, Graphing Plane Curves, Precalculus
Parametrization of Curves | Numericals | Vector Calculus | Maths
Multivariable calculus 1.1.2: Introduction to parametrized curves
Introduction to parametrizing a surface with two parameters | Multivariable Calculus | Khan Academy
Multivariate Calculus (Lecture 16): Parametric Curves
Parameterization of a Function
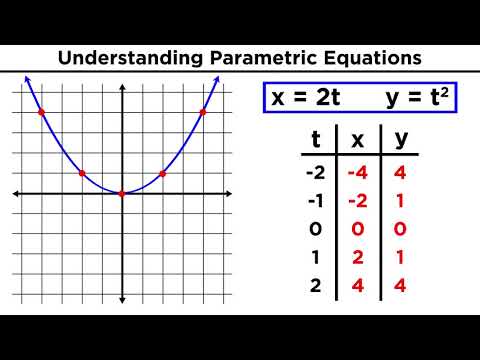
Parametric Equations
Describing Surfaces Explicitly, Implicitly & Parametrically // Vector Calculus
Paths and Parametric Curves // Multivariable Calculus // Short Lecture
Tangent Line to a Parametrized Curve
Example of Arc Length Along a Parametrized Curve
Calculus 3 Lecture 12.3: Arc Length/Parameterization, TNB (Frenet-Serret) Intro
Multivariable calculus 1.1.3: More techniques for sketching parametrized curves
Multivariable Calculus - Ch. 9.1 & 10.7 - Examples of 3D Parametric Curves, Parametrization
Multivariable Calculus: Curvature κ(t) for a parametrized curve
Calculus 3: Vector Calculus in 3-D (6 of 35) Parametric Equations and Vectors: Example 1
Arc Length of Parametric Curves
Комментарии
 0:05:51
0:05:51
 0:10:04
0:10:04
 0:11:54
0:11:54
 0:06:34
0:06:34
 1:38:26
1:38:26
 0:02:39
0:02:39
 1:08:39
1:08:39
 0:33:29
0:33:29
 0:12:09
0:12:09
 0:13:48
0:13:48
 0:19:03
0:19:03
 1:39:24
1:39:24
 0:02:04
0:02:04
 0:04:36
0:04:36
 0:11:05
0:11:05
 0:14:10
0:14:10
 0:03:45
0:03:45
 0:03:40
0:03:40
 2:12:45
2:12:45
 0:09:12
0:09:12
 0:16:38
0:16:38
 0:17:36
0:17:36
 0:02:58
0:02:58
 0:12:34
0:12:34