filmov
tv
Sketching a Parametrized Curve

Показать описание
Multivariable Calculus: Sketch the curve for the vector-valued function r(t) = (cos(t), sin(t), -cos(t)-sin(t) +1). We describe the trace of the curve as the intersection of a cylinder and a plane.
For more videos like this one, please visit the Multivariable Calculus playlist at my channel.
For more videos like this one, please visit the Multivariable Calculus playlist at my channel.
Sketching a Parametrized Curve
Parametric Equations Introduction, Eliminating The Paremeter t, Graphing Plane Curves, Precalculus
Parametric Curves - Basic Graphing
Parametric Equations : Curve Sketching (1) : ExamSolutions
Parametric curves | Multivariable calculus | Khan Academy
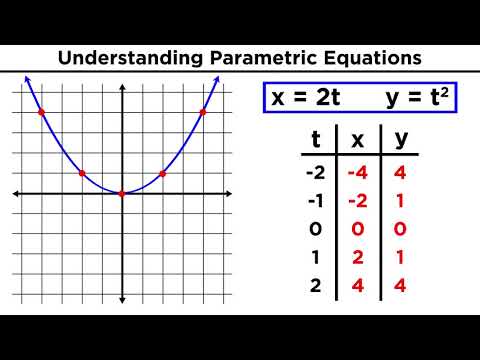
Parametric Equations
Parametric Equations Sketching a Curve (3 Examples)
Sketch a Parametric Curve
Grasshopper Kangaroo (Parametric Shell) #shorts
Sketch the Curve Generated by the Parametric Equations
Sketch the Graph of the Parametric Equations, Indicate Orientation, and Write the Rectangular Form
How to Parametrize a Curve
How to sketch parametric curves and their orientation
Calculus 2 Lecture 10.2: Introduction to Parametric Equations
Matching Parametric Graphs with Parametric Equations: Stewart Chapter 13 Problems 21-26, 13.21
Parametric Equations : Curve Sketching (2) : ExamSolutions
Multivariable calculus 1.1.3: More techniques for sketching parametrized curves
Parametrization of Plane Curves
Video 2051.15 Sketching parametric curves
Sketching Parametric Curves
Edexcel A level Maths: 8.3 Sketching Parametric Curves
Stewart, 10.1.26: Reconstruct Parametric graphs from graphs x(t) and y(t)
MATH 2414 - Parametric Curves (04): Another Example of Sketching a Curve, Eliminating the Parameter
How to Sketch Parametric Curves in xy-plane
Комментарии
 0:02:39
0:02:39
 0:33:29
0:33:29
 0:08:46
0:08:46
 0:10:20
0:10:20
 0:05:51
0:05:51
 0:04:36
0:04:36
 0:05:09
0:05:09
 0:03:38
0:03:38
 0:00:51
0:00:51
 0:05:51
0:05:51
 0:05:12
0:05:12
 0:06:34
0:06:34
 0:11:18
0:11:18
 1:38:26
1:38:26
 0:07:37
0:07:37
 0:09:17
0:09:17
 0:09:12
0:09:12
 0:11:55
0:11:55
 0:08:31
0:08:31
 0:07:14
0:07:14
 0:05:32
0:05:32
 0:04:42
0:04:42
 0:05:14
0:05:14
 0:02:11
0:02:11