filmov
tv
Simplify Expressions Basic Problems

Показать описание
Learn how to simplify basic expressions
Example problems include 6x +3y +4x-2y -8x
5(x+4) - ( x+7)
The key is to combine like terms and follow the correct order of operations.
You can use PEMDAS to help with the correct order of operations.
Example problems include 6x +3y +4x-2y -8x
5(x+4) - ( x+7)
The key is to combine like terms and follow the correct order of operations.
You can use PEMDAS to help with the correct order of operations.
Simplify Expressions Basic Problems
How to Simplify an Expression: A Beginner's Guide | Algebraic Expressions | Math with Mr. J
Simplify Grade 10 Algebraic Expressions
Simplify Algebraic Expressions: a(x+b)-c(x-d)
Simplifying Expressions
Simplifying Algebraic Expressions - Laws of Exponents @MathTeacherGon
Grade 9 Simplifying expressions: Algebra exam questions
Simplifying Algebraic Expressions with Parentheses: A Beginner’s Guide | Algebra | Math with Mr. J
Simplifying Algebraic Expressions: Top Exam Tricks & MCQs | For GCSE, Grade 10, SSC
Simplifying Exponents With Fractions, Variables, Negative Exponents, Multiplication & Division, ...
01 - Simplify Expressions w/ Exponents in Algebra (Quotients of Monomials) - Part 1
Simplifying Rational Expressions
Art of Problem Solving: Simplifying Linear Expressions
Simplifying Expressions using Distributive Property | Expression & Equations | Grade 6
Simplify Class 8 | How To Simplify | Simplifying Algebraic Expressions | Simplification
Simplify Basic Algebraic Expressions: Negative Numbers - VividMath.com
Simplify | Simplifying Algebraic Expressions | Simplify Class 8
Algebraic Expressions (Basics)
Simplifying Equations using Distributive Property | Expressions & Equations | Grade 6
Simplify rational expression using the rules of exponents
Simplifying Algebraic Expressions - Grade 8/Stage 8 Mathematics
GCSE Maths - How to Simplify Expressions by Collecting Like Terms #28
How to Simplify Rational Expressions in Algebra
Simplifying rational expressions introduction | Algebra II | Khan Academy
Комментарии
 0:04:15
0:04:15
 0:55:18
0:55:18
 0:07:45
0:07:45
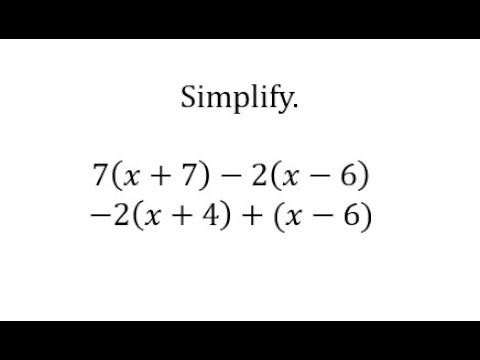 0:02:46
0:02:46
 0:08:31
0:08:31
 0:08:58
0:08:58
 0:30:32
0:30:32
 0:07:12
0:07:12
 0:11:18
0:11:18
 0:11:48
0:11:48
 0:30:28
0:30:28
 0:11:08
0:11:08
 0:04:50
0:04:50
 0:02:09
0:02:09
 0:01:28
0:01:28
 0:01:57
0:01:57
 0:03:26
0:03:26
 0:09:56
0:09:56
 0:04:18
0:04:18
 0:07:50
0:07:50
 0:03:29
0:03:29
 0:04:41
0:04:41
 0:01:00
0:01:00
 0:07:28
0:07:28