filmov
tv
Quadratic Trigonometric Equations
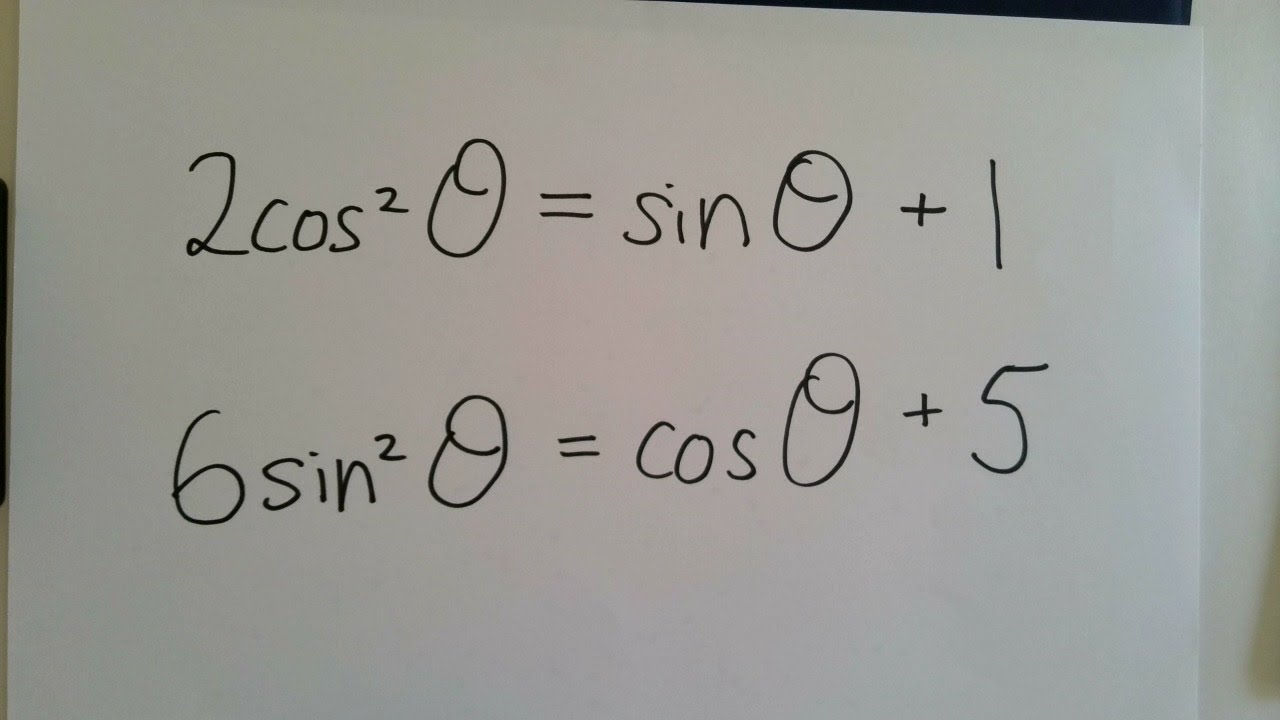
Показать описание
Solving trig equations using identities
0:00 Intro
0:23 Simple example
5:50 Example 2
6:52 Identity
16:30 Example 3
24:05 tan question
0:00 Intro
0:23 Simple example
5:50 Example 2
6:52 Identity
16:30 Example 3
24:05 tan question
Solving Trigonometric Equations By Factoring & By Using Double Angle Identities
Solving Quadratic Trigonometric Equations
Solve a Trig Equation in Quadratic Form Using the Quadratic Formula (Cosine, 2 Solutions)
Quadratic Trigonometric Equations | Mr Mathematics.com
Solve Quadratic Trigonometric Equation in Tan Using Factoring
Solving Quadratic Trigonometric Equations
Solving Trigonometric Equations Using the Quadratic Formula - Example 2
Solve Quadratic Trigonometric Equation 1 after Factoring MHF4U
Trigonometric equations bsc 1st year | bsc 1st year math algebra and trigonometry | Mathslighthouse
Solve Trigonometric Equation in Tan with Quadratic Formula
Quadratic Trigonometric Equations General Solution Strategy
Ex: Solve a Factorable Trig Equation with Rounded Radian Solutions - Quadratic Form
How to apply factoring to solve a trigonometric equation
Quadratic Trigonometric Equations
Ex: Solve a Trigonometric Equation Using Substitution and the Quadratic Formula
Solving a trigonometric equation by factoring
Find the solutions to a trig equation between 0 and 2pi
Solving Trigonometric Equations
How to solve a quadratic trigonometric equation
5.4 Solving Quadratic Trig Equations (full lesson) | MHF4U
Solve Quadratic Trigonometric Equation in Factored Form 2
Advanced Functions 7.6 Solving Quadratic Trigonometric Equations
Solving Trigonometric Equations Using the Quadratic Formula - Example 1
Trigonometric Equations in Quadratic Form
Комментарии
 0:18:32
0:18:32
 0:16:44
0:16:44
 0:05:25
0:05:25
 0:08:57
0:08:57
 0:04:24
0:04:24
 0:05:53
0:05:53
 0:08:46
0:08:46
 0:05:16
0:05:16
 0:44:27
0:44:27
 0:05:51
0:05:51
 0:08:42
0:08:42
 0:06:01
0:06:01
 0:10:34
0:10:34
 0:24:41
0:24:41
 0:07:54
0:07:54
 0:05:19
0:05:19
 0:03:38
0:03:38
 0:15:22
0:15:22
 0:04:21
0:04:21
 0:45:02
0:45:02
 0:04:48
0:04:48
 0:17:26
0:17:26
 0:03:57
0:03:57
 0:13:04
0:13:04