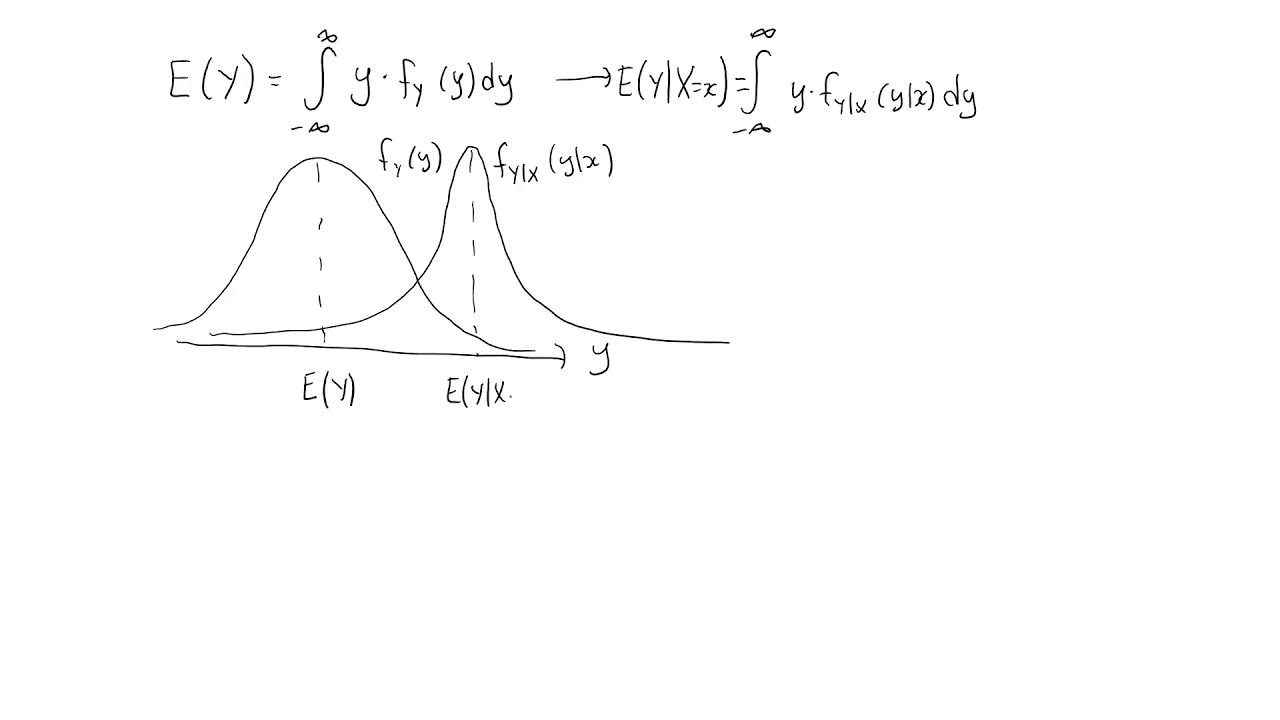
Conditional expectations, continuous random variables

preview_player
Показать описание

  1. Jochumzen
Рекомендации по теме
Conditional expectations, continuous 0:08:21

Conditional expectations, continuous random variables

Conditional Expectation of 0:08:34

Conditional Expectation of Random Variables: Example 1

Examples of Conditional 0:23:46

Examples of Conditional Expectation for Discrete and Continuous Case

L13.2 Conditional Expectation 0:04:31

L13.2 Conditional Expectation as a Random Variable

Conditional expectations, continuous 0:08:21

Conditional expectations, continuous random variables

Conditional expectation -- 0:03:22

Conditional expectation -- Example 1

Conditional expectation of 0:07:46

Conditional expectation of a function of a random variable

Conditional Probability given 0:12:02

Conditional Probability given Joint PDF

Continuous Probability Distributions 0:32:03

Continuous Probability Distributions -- Video 1 of Lesson 3

Find coveriance, coefficient 0:29:37

Find coveriance, coefficient of correlation, Conditional Expectation,Variance of Continuous r.v,

[Chapter 6] #9 0:08:34

[Chapter 6] #9 Conditional distribution, the continuous case

Conditional Distributions: Expectations 0:03:07

Conditional Distributions: Expectations

[Chapter 7] #5 0:20:34

[Chapter 7] #5 Conditional expectation

Discrete Random Variables 0:14:04

Discrete Random Variables - Conditional Expectation I

Conditioning of Continuous 0:11:12

Conditioning of Continuous Random Variables

Conditional Expectation of 0:08:25

Conditional Expectation of Exponential

Conditional Expectations(Continuous Case) 0:02:50

Conditional Expectations(Continuous Case)

Lecture 26 Conditional 0:47:49

Lecture 26 Conditional Expectation + Sum of Two Random Variables

Expected Value of 0:06:16

Expected Value of X with joint PDF

Conditional expectations, discrete 0:11:37

Conditional expectations, discrete random variables

[Chapter 6] #8 0:13:37

[Chapter 6] #8 Conditional distribution, the discrete case

Conditional Expectation-I 0:34:38

Conditional Expectation-I

PB52: Conditional PDFs 0:08:46

PB52: Conditional PDFs for Continuous Joint Random Variables

Probability Video 3.4: 0:15:55

Probability Video 3.4: Continuous Random Variables - Conditional Probability Models

Комментарии
Автор

Thank you so much for your lecture.. I was almost crazy since I kept failed to find right CEF. Now
I can finally finish my assignment after watching your video. Thank you so much😭😭😭😭😭😭😭😭😭love from
Korea💙💙

qbrpupo
Автор

You are a lifesaver, Especially the part about conditional expectations and their dependence.

Question: At 6:20, why is the integral over dy and not dx?

advaitathreya
Автор

Last part about f_z(z)...I'm not sure about my step 0
2 step procedure: 1)find CDF of Z. 2)differentiate to get PDF of Z

-1) find f_X. Just integrate the joint (f(x, y) = x+y) with respect to y...or, by symmetry it's similar to the f_Y in the video. f_X = x +1/2

0) finding the inverse
From (3X+2)/(6X+3) <= z, make X the subject
3X+2 <= 6zX+3z
2-3z <= (6z-3)X
Assuming 6z-3 < 0 (i.e. z < 1/2)
(2-3z) / (6z-3) >= X (flip the inequality bcos i divided by a negative quantity)


1) CDF of Z
= F_z
= P(Z<= z)
= P((3X+2)/(6X+3) <= z)
= P(X <= (2-3z) / (6z-3)) (from step 0)
= F_X ((2-3z) / (6z-3))
= CDF of X, but evaluated at (2-3z) / (6z-3)

2) PDF of z
= d/dz [ F_X ((2-3z) / (6z-3)) ]
= f_X ((2-3z) / (6z-3)) * d/dz [ (2-3z) / (6z-3) ]
= ((2-3z) / (6z-3) + 1/2 ) * d/dz [ (2-3z) / (6z-3) ]
=...
=-1/18(2z-1)^3

But..am I allowed to assume that z<1/2 in step 0 ?

khbye