filmov
tv
Number of generators of Finite Cyclic Group - Application of Euler's fai function -Group theory

Показать описание
Join this channel to get access to perks:
............ Join this channel to get access to perks:
Here in this video i will explain how to find the number of generators of finite cyclic group and this is the application of the concept of Euler's phi function. This is a very important concept of Group Theory.
If you are looking out for any of these queries then solution is here:
1) Cyclic group generator element
2) how to find generating element
3) Number of generators of finite cyclic group
4) application of Euler's fai function
5) number of generators of a cyclic group of order n
6) number of generators of a group
7) how to find number of generators of a cyclic group
8) eulier's phi function application
9) euler's phi function is the number of positive numbers which are less than n and relatively co prime to n.
welcome you all in my channel LEARN MATH EASILY
Link for this video is as follows:
This video will be very useful if you are student of Higher Classes in mathematics like B.Sc, M.Sc , Engineering and if you are preparing for UGC Net and iit Jam etc.
Please Do not forget to Like, Share and Subscribe
Before this topic i did various other topics of Real Analysis:
My other Videos are as follows:
Metric Space
Countable and Uncountable Sets
Supremum & Infimum
Connectedness - Real Analysis
Compactness
Neighbourhoods and Limit Points- Real Analysis
Infinite Sequences - Real analysis
Indeterminate forms and l’hospital’s rule
Multiplication Tables- Shortcut tricks
Shortcut tricks to Solve linear equations
Quadratic Equations
Square and Cube Shortcuts
Number System
HCF And LCM
Multiplication Tricks
Subscribe to My YouTube Channel " Learn Math Easily" :
.................................................
My Page on Facebook:
.......................................................
#NumberofgeneratorsofFiniteCyclicGroup #Euler'sφ(n)Function #EulerphiFunciton
............ Join this channel to get access to perks:
Here in this video i will explain how to find the number of generators of finite cyclic group and this is the application of the concept of Euler's phi function. This is a very important concept of Group Theory.
If you are looking out for any of these queries then solution is here:
1) Cyclic group generator element
2) how to find generating element
3) Number of generators of finite cyclic group
4) application of Euler's fai function
5) number of generators of a cyclic group of order n
6) number of generators of a group
7) how to find number of generators of a cyclic group
8) eulier's phi function application
9) euler's phi function is the number of positive numbers which are less than n and relatively co prime to n.
welcome you all in my channel LEARN MATH EASILY
Link for this video is as follows:
This video will be very useful if you are student of Higher Classes in mathematics like B.Sc, M.Sc , Engineering and if you are preparing for UGC Net and iit Jam etc.
Please Do not forget to Like, Share and Subscribe
Before this topic i did various other topics of Real Analysis:
My other Videos are as follows:
Metric Space
Countable and Uncountable Sets
Supremum & Infimum
Connectedness - Real Analysis
Compactness
Neighbourhoods and Limit Points- Real Analysis
Infinite Sequences - Real analysis
Indeterminate forms and l’hospital’s rule
Multiplication Tables- Shortcut tricks
Shortcut tricks to Solve linear equations
Quadratic Equations
Square and Cube Shortcuts
Number System
HCF And LCM
Multiplication Tricks
Subscribe to My YouTube Channel " Learn Math Easily" :
.................................................
My Page on Facebook:
.......................................................
#NumberofgeneratorsofFiniteCyclicGroup #Euler'sφ(n)Function #EulerphiFunciton
Комментарии
 0:10:38
0:10:38
 0:00:58
0:00:58
 0:00:11
0:00:11
 0:13:03
0:13:03
 0:00:54
0:00:54
 0:13:42
0:13:42
 0:15:30
0:15:30
 0:06:26
0:06:26
 0:29:23
0:29:23
 0:00:55
0:00:55
 0:18:34
0:18:34
 0:11:03
0:11:03
 0:00:59
0:00:59
 0:09:03
0:09:03
 0:04:42
0:04:42
 0:00:55
0:00:55
 0:03:23
0:03:23
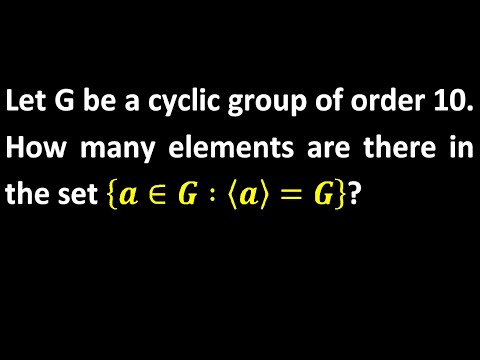 0:05:39
0:05:39
 0:29:00
0:29:00
 0:09:01
0:09:01
 0:05:26
0:05:26
 0:12:27
0:12:27
 0:11:32
0:11:32
 0:01:01
0:01:01