Cyclic Groups, Generators, and Cyclic Subgroups | Abstract Algebra

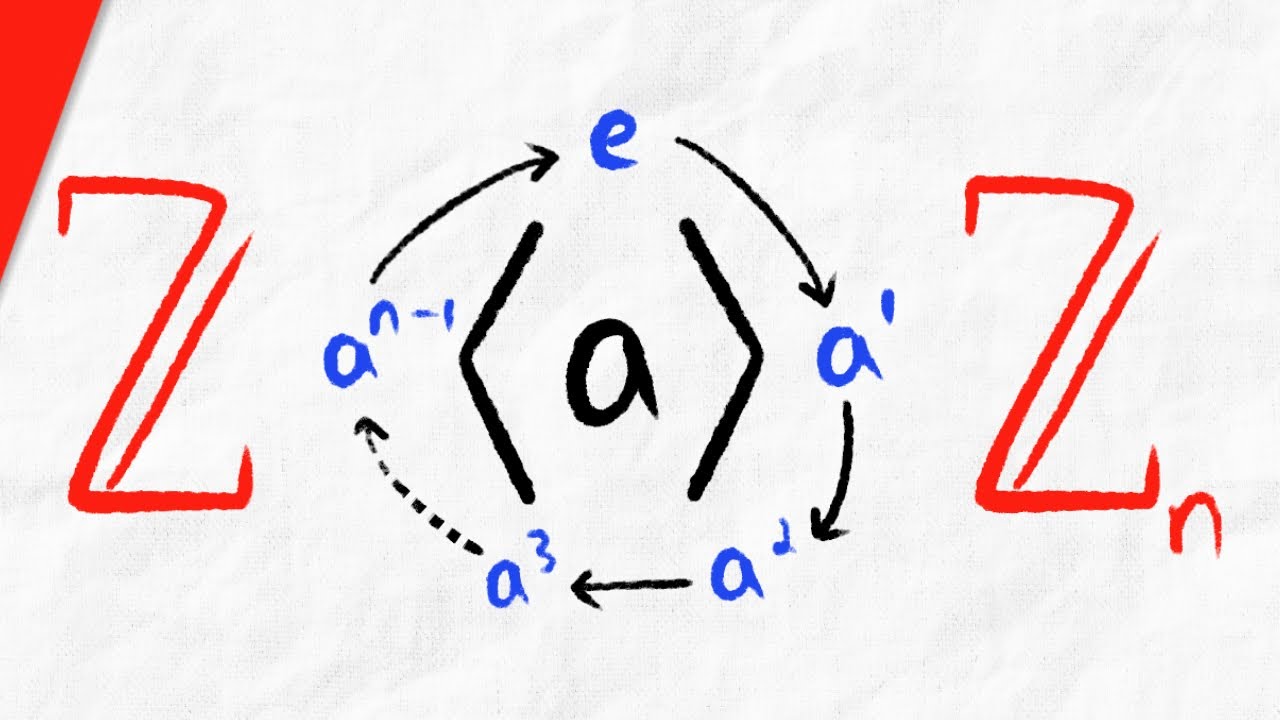
We introduce cyclic groups, generators of cyclic groups, and cyclic subgroups. We discuss an isomorphism from finite cyclic groups to the integers mod n, as well as an isomorphism from infinite cyclic groups to the integers. We establish a cyclic group of order n is isomorphic to Zn, and an infinite cyclic group is isomorphic to the integers. Finally, we introduce cyclic subgroups, and show the powers of an element will always form a cyclic subgroup. #abstractalgebra #grouptheory

Abstract Algebra Exercises:

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

[rosskious]

Abstract algebra is really easy if you are willing to “ not tie your mind to past concepts and their definitions “. The math is extremely easy, but you have to let your mind adjust to new and different ideas and ways of doing things. Mixing visual, hands on problems and theory together in the lessons helps that hurdle .

[HiranyakshaDas]

Fantastic explanation of cyclic groups and their isomorphisms! You really made the concept of generators and cyclic subgroups so clear and accessible. I especially appreciated how you demonstrated the isomorphisms with both finite and infinite cyclic groups, and the way you showed that the powers of an element always form a cyclic subgroup was super insightful. This video is a great resource for anyone diving into group theory. Thank you for making such complex topics understandable and engaging!

[ThefamousMrcroissant]

Another wonderful lecture. Second time I stumbled upon your content through my recommended feed. Pretty sure I already commented on your other video but you are a real standout among teachers in how coherent and neat your lectures tend to be. Solid script, good pacing, clear articulation. Keep up the excellent work!

[erinmeyers-tw]

Thank you for your videos, they really help me grasp these topics!! I wondered if you could please do a video on cyclic subgroups, the greatest common divisor, prime numbers, and all that mess? It's very confusing to me!

[verrokade]

Perfect explained! Thank you soo much!!

[kreskimatmy]

i just love your videos, thank you for this

[Laura-vjzd]

Thank you for this video :) it helped a lot

[MrCoreyTexas]

Challenge at 2:36 is 5, 5 generates 5, 2, 7, 4, 1, 6, 3, 0 then repeats

[jeremymorgan]

1:22 - what is the definition for a generator under addition? this is so confusing to have the definition for G, and then immediately a new concept that's not defined is presented

[liketsontobo]

I've always said this, you are the best

[moneyhoney_]

Where did you get that trigonometry hoodie

[eduyantra]

How will you generate negative integers using the generator <1> ?? Please help

[PhdScholar]

Sir please share some examples of Cyclic groups like Z10 Z15 like

[djehutisundaka]

(2^0) = SU(1)
(2^1) = U(1)
(2^2) = U(2)
(2^3) = SU(3)

[standarddeviation]

Where are you getting 10, 5, and 8? 2:26

[springvibes]

I just login to say thank you very much, your classes are the best!!! Hero of nice explaining 🤍 thank u & wish u the best