filmov
tv
RNT1.4.1. Example of Quotient Ring

Показать описание
Abstract Algebra: Are there fields F such that the rings F[x]/(x^2) and F[x]/(x^2-1) are isomorphic? We construct an isomorphism when char F = 2.
RNT1.4.1. Example of Quotient Ring
RNT1.4. Ideals and Quotient Rings
Example of Factor / Quotient Ring (Z/4Z)
302.10B: Fields as Quotients of Rings
VLOG Some Examples of Quotient Rings
Some Quotient Rings Basics
Basics of Quotient Rings
Quotient rings
22-Quotient Ring and its example
Abstract Algebra 13.4: A Polynomial Factor Ring
Abstract Algebra Ring Homomorphisms Quotient Rings
Quotient Rings as Integral Domains
49 The Quotient Ring R/S
Ring Examples (Abstract Algebra)
Ideals in Ring Theory (Abstract Algebra)
Quotient Rings Part 1
Abstract Algebra | 19. Quotient Rings
L 27 Quotient Ring || Factor Ring | Ring Theory and Linear Algebra 1 | B Sc Hons Maths DU
Commutative Algebra 18, Quotient Rings
An Example of Left-Cosets and a Quotient Ring
IdealsIII
Quotient Rings and the First Isomorphism Theorem for Rings (Algebra 1: Lecture 28 Video 1)
RNT1.2.1. Example of Integral Domain
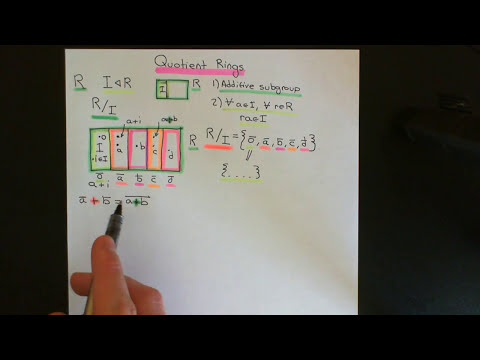
Quotient Rings
Комментарии
 0:05:07
0:05:07
 0:20:47
0:20:47
 0:22:31
0:22:31
 0:16:19
0:16:19
 0:21:06
0:21:06
 0:07:44
0:07:44
 0:03:10
0:03:10
 0:20:16
0:20:16
 0:59:05
0:59:05
 0:08:25
0:08:25
 0:08:02
0:08:02
 0:10:49
0:10:49
 0:14:44
0:14:44
 0:07:18
0:07:18
 0:11:57
0:11:57
 0:25:52
0:25:52
 0:51:38
0:51:38
 0:23:09
0:23:09
 0:08:56
0:08:56
 0:07:05
0:07:05
 0:12:09
0:12:09
 0:20:04
0:20:04
 0:07:07
0:07:07
 0:09:05
0:09:05