RNT1.4. Ideals and Quotient Rings

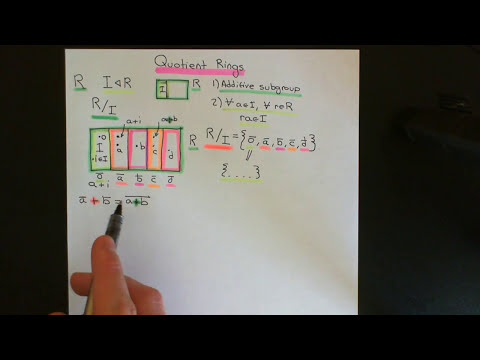
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.

[flehue]

I realized he was sit and my head exploded

[theleastcreative]

Are you teaching at a University? I am consistently blown away by your ability to explain abstract algebra so clearly

[bentupper]

First time ever hearing the phrase, "Old school group theory"!

[Tipsi-mobl]

Thank you for this great explanation!
However, I still have got a question: How do Z[x]/(x^2+1) and Z[x]/(3x^2+3) look like? Is the first one isomorphic to Z[i] (because i^2+1=0)?

[INDIANANA]

I have a question.

At 6:39 we are are establishing that the kernel of phi can't be the whole of R because R is one- one.

But aren't we actually trying to prove that phi must be one-one?

will this argument work?

kernel of phi can't be R because it would mean that Phi(1)= 0 which contradicts the property of ring homomorphism that phi(1)= 1 ?

hence, the kernel of phi can't be the whole of R. this establishes that kernel has to be 0. therefore the ring homomorphism is one-one.

will this argument work ?

[michaelduah]

MathDoctorBob,
pls help me with this question also,
1 .show that A is an ideal of A+B
2. show that A=A+A for some ideal A in R
thnx

[idobooks]

Thanks :) Is F considered an Ideal under F[x]?
If yes how do I prove this?

[Gipsyu]

Thanks, good work, very helpful great explanation.

[carolinenamanya]

hey, thank you for the video, is there a difference between a ring of quotients and a quotient ring?

[surferdudevideo]

How do you, "Shift according to the lattice" to get 2i=-1 and 2+i=4 .... and in general?

Thanks, great videos btw! I may pass my class now!

[aarohgokhale]

0:30 Shouldn't you get that phi(0) = 0 from the first property alone?

phi(a + 0) = phi(a) + phi(0) = phi(a)

Then phi(0) = 0

[galuharanastiti]

why use ideal for quotient ring? why not use subring? please explain to me. thank you

[hoangtudaden]

not really a ring associate bc assoc. is already a property(+, *) of ring. what you meant is ring with identity.

[ritcher]

This guy sounds like Nick Cage. Bad ass!