filmov
tv
Physics 40 Resistivity and Resistance (16 of 32) Resistance of a Cylinder with Cut-Out

Показать описание
In this video I will find resistance of a cylinder with a truncated cone cut-out and varying resistivity.
Physics 40 Resistivity and Resistance (17 of 33) Resistivity and Temperature
Physics 40 Resistivity and Resistance (19 of 33) What is Super Conductivity?
Physics 40 Resistivity and Resistance (32 of 33) Effects of Volt & Current Meter
Physics 40 Resistivity and Resistance (23 of 33) V=? Where L=50m, D=1.02mm, and I=5A
Physics 40 Resistivity and Resistance (22 of 33) V=? Between 2 pts on a Conductor with Current
Physics 40 Resistivity and Resistance (30 of 33) Effects of Volt & Current Meter (Open Circuit...
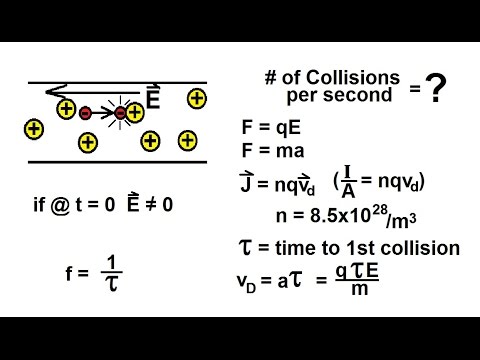
Physics 40 Resistivity and Resistance (21 of 33) # of Collision per Second = ?
Physics 40 Resistivity and Resistance (31 of 33) Effects of Volt & Current Meter
Physics 40 Resistivity and Resistance (20 of 33) Super Conductivity at a Quantum Mechanic State
Physics 40 Resistivity and Resistance (25 of 33) Current in an Incomplete Circuit
Physics 40 Resistivity and Resistance (24 of 33) How to Minimize Voltage Drop?
Physics 40 Resistivity and Resistance (11 of 32) Power Dissipation with Changing Currents
Physics 40 Resistivity and Resistance (12 of 32) Current Density of a Conductor
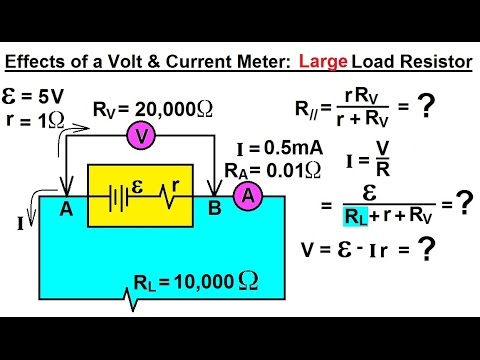
Physics 40 Resistivity and Resistance (33 of 33) V=? Across a Large Load Resistor
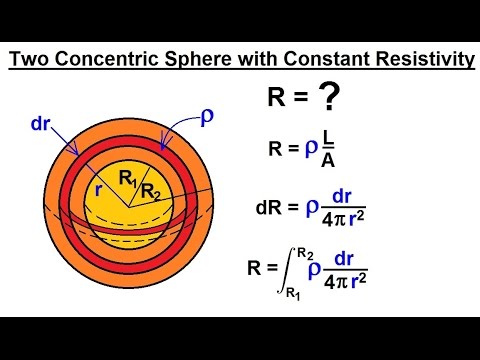
Physics 40 Resistivity and Resistance (14 of 32) Resistance Between 2 Concentric Spheres
Physics 40 Resistivity and Resistance (10 of 32) Resistor Color Code Explained
Physics 40 Resistivity and Resistance (27 of 33) Find the Potential Difference of a Circuit
Resistivity and Resistance Formula, Conductivity, Temperature Coefficient, Physics Problems
Physics 40 Resistivity and Resistance (18 of 33) R=? of a 50m Copper Wire at T=0C and 100C
Physics 40 Resistivity and Resistance (16 of 32) Resistance of a Cylinder with Cut-Out
Physics 40 Resistivity and Resistance (15 of 32) Resistance Between 2 Concentric Spheres
Physics 40 Resistivity and Resistance (26 of 33) What is an Electromotive 'Force', EMF
Physics 40 Resistivity and Resistance (13 of 32) Resistivity in Light Bulbs
Physics 40 Resistivity and Resistance (29 of 33) Exploring Electromotive Force, EMF, Graphically
Комментарии
 0:07:47
0:07:47
 0:05:34
0:05:34
 0:05:32
0:05:32
 0:03:04
0:03:04
 0:04:12
0:04:12
 0:05:38
0:05:38
 0:09:48
0:09:48
 0:05:34
0:05:34
 0:04:51
0:04:51
 0:03:06
0:03:06
 0:04:46
0:04:46
 0:03:21
0:03:21
 0:04:28
0:04:28
 0:06:20
0:06:20
 0:04:52
0:04:52
 0:04:18
0:04:18
 0:03:57
0:03:57
 0:21:35
0:21:35
 0:06:42
0:06:42
 0:16:34
0:16:34
 0:06:50
0:06:50
 0:04:41
0:04:41
 0:13:16
0:13:16
 0:04:37
0:04:37