filmov
tv
Linear ODEs: Resonance and Repeated Roots
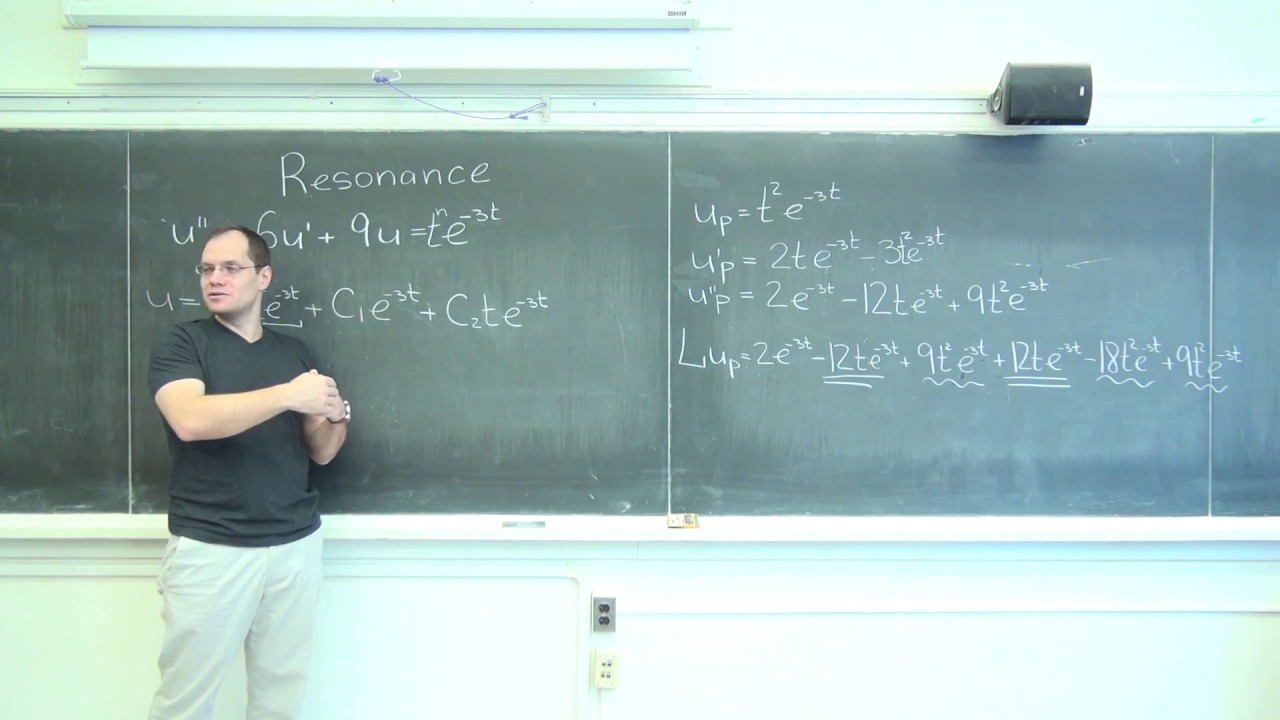
Показать описание
Linear ODEs: Resonance and Repeated Roots
Linear ODEs with Constant Coefficients: Repeated Roots
Linear ODEs with Constant Coefficients: Illustration of Resonance with Exponentials
Linear ODEs with Constant Coefficients: Classical Resonance
Resonance | Lecture 24 | Differential Equations for Engineers
Resonance Example D^4y=1=e^(0t)
Undetermined Coefficients: Solving non-homogeneous ODEs
Mechanical Vibrations: Underdamped vs Overdamped vs Critically Damped
Inhomogeneous Differential Equation
World's Simplest ODE is Still Interesting!
Method of Undetermined Coefficients - Nonhomogeneous 2nd Order Differential Equations
Oxford student reacts to India’s JEE Advanced exam paper *really hard* #shorts #viral #jeeadvanced
Differential Equations - Forced Oscillations - Resonance
Resonance
Using Calculus to Explain Resonance
Understanding Vibration and Resonance
Overview of Resonance Phenomena
JEE Aspirants ka Sach 💔 #JEE #JEEMain #Shorts
Differential Equations: resonance and damping discussion, 9-26-17
Ordinary Differential Equations - Force Mechanical Vibration & Resonance
Resonance -- Just where does that 't' come from?
Inhomogeneous, second-order, constant-coefficient ode
ODE Lecture 16 Beats and Resonance
Stability and Eigenvalues: What does it mean to be a 'stable' eigenvalue?
Комментарии
 0:04:19
0:04:19
 0:08:03
0:08:03
 0:08:26
0:08:26
 0:15:42
0:15:42
 0:13:38
0:13:38
 0:08:22
0:08:22
 0:12:44
0:12:44
 0:11:16
0:11:16
 0:08:58
0:08:58
 0:04:00
0:04:00
 0:41:28
0:41:28
 0:01:00
0:01:00
 0:05:58
0:05:58
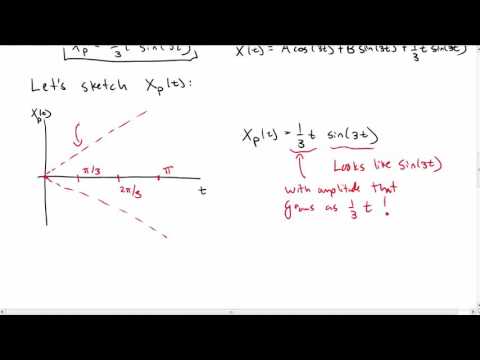 0:09:02
0:09:02
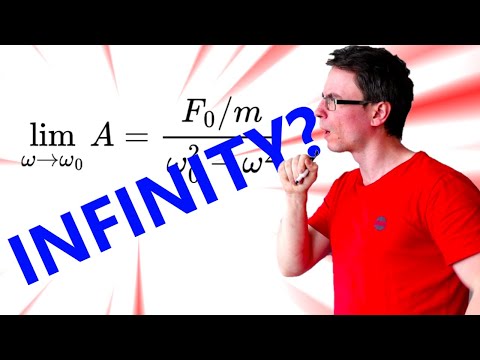 0:04:40
0:04:40
 0:19:42
0:19:42
 0:05:52
0:05:52
 0:00:12
0:00:12
 0:46:42
0:46:42
 0:46:22
0:46:22
 0:10:01
0:10:01
 0:07:13
0:07:13
 0:12:59
0:12:59
 0:14:53
0:14:53