filmov
tv
Quotient Rule Proof

Показать описание
In this video, I show you how to proof the Quo Chen Lu formula (aka Quotient Rule) from the Prada Lu and the Chen Lu (aka Product Rule and the Chain Rule).
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Please subscribe for more math content!
Check out my site & social media
Thank you for your support!
blackpenredpen | 曹老師
Quotient Rule Proof
Proof of The Quotient Rule
Quotient rule from product & chain rules | Derivative rules | AP Calculus AB | Khan Academy
COOL Quotient Rule Proof
Quotient Rule Proof
How to derive the QUOTIENT RULE from scratch
Quotient Rule Proof: How to Prove The Quotient Rule from the Product Rule and Chain Rule
The Quotient Rule - Intuitive Proof
The Product Rule Proof
Proof of Quotient Rule
a unifying product quotient rule proof
How do we prove the quotient rule? - Week 5 - Lecture 11 - Mooculus
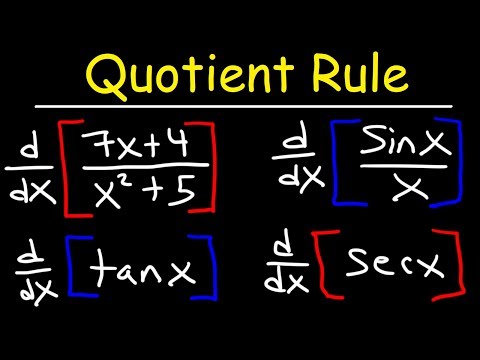
Quotient Rule For Derivatives
PROOF of Quotient Rule of Differentiation
Proving the Quotient Rule of Differentiation #shorts
Proof of the Quotient Rule Explained | Algebra Tutor
quotient rule proof 1st principles 20016
Calculus 3.07i - The Quotient Rule
Deriving the Quotient Rule from first principles
Quotient Rule for Derivatives - Proof (Using the Product and Reciprocal Rule)
Quotient rule proof using the chain and product rules - Calculus
How to Prove and Use the Quotient Rule of Differentiation | Calculus
Quotient Rule Proof
Quotient Rule
Комментарии
 0:05:05
0:05:05
 0:06:53
0:06:53
 0:05:15
0:05:15
 0:04:53
0:04:53
 0:07:36
0:07:36
 0:05:33
0:05:33
 0:04:44
0:04:44
 0:06:11
0:06:11
 0:01:37
0:01:37
 0:07:46
0:07:46
 0:03:22
0:03:22
 0:05:02
0:05:02
 0:11:55
0:11:55
 0:06:16
0:06:16
 0:00:55
0:00:55
 0:00:32
0:00:32
 0:09:26
0:09:26
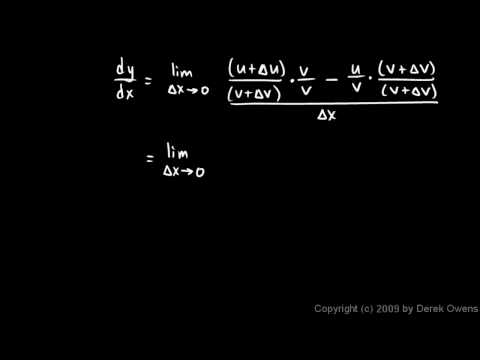 0:10:59
0:10:59
 0:09:38
0:09:38
 0:03:08
0:03:08
 0:08:06
0:08:06
 0:16:08
0:16:08
 0:12:04
0:12:04
 0:08:13
0:08:13