David Jerison: Localization of eigenfunctions via an effective potential

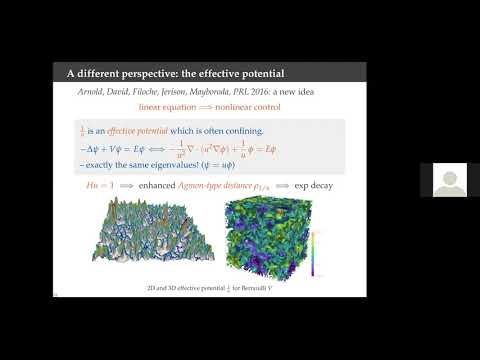
Abstract: We discuss joint work with Doug Arnold, Guy David, Marcel Filoche and Svitlana Mayboroda. Consider the Neumann boundary value problem for the operator L=divA∇+V on a Lipschitz domain Ω and, more generally, on manifolds with and without boundary. The eigenfunctions of L are often localized, as a result of disorder of the potential V, the matrix of coefficients A, irregularities of the boundary, or all of the above. In earlier work, Filoche and Mayboroda introduced the function u solving Lu=1, and showed numerically that it strongly reflects this localization. In this talk, we deepen the connection between the eigenfunctions and this landscape function u by proving that its reciprocal 1/u acts as an effective potential. The effective potential governs the exponential decay of the eigenfunctions of the system and delivers information on the distribution of eigenvalues near the bottom of the spectrum.

Recording during the thematic meeting "Harmonic Analysis and Geometric Measure Theory" the October 5, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France)

Filmmaker: Guillaume Hennenfent

- Chapter markers and keywords to watch the parts of your choice in the video
- Videos enriched with abstracts, bibliographies, Mathematics Subject Classification
- Multi-criteria search by author, title, tags, mathematical area