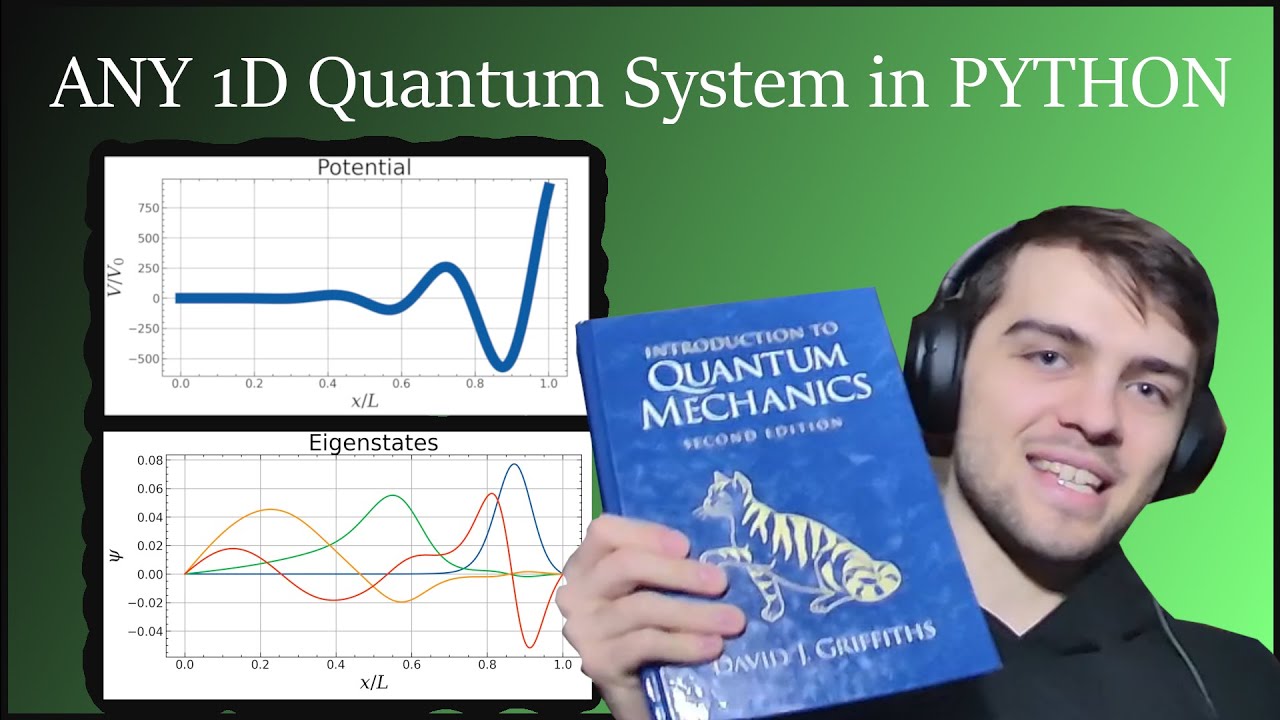
Eigenstates of ANY 1D Potential in PYTHON

Remember having to solve problems analytically? What a pain. With python you can solve for any potential you want.

Code located in the link below. Go to "Python Metaphysics tutorials" and then "Vid 3"

[eduardoh.m]

You sir, you are a freaking beast! Keep it up and I'll be here every single time!

[josephjones]

When done in discrete form like this it reminds me of solving a system of lots of masses connected by springs. You get an almost identical tradiagonal matrix

[AJ-etvf]

So awesome! Watching your Python videos is just so immensely intellectually satisfying, inspiring, and galvanizing. Love your videos. The value of your videos cannot be overstated.

[chng]

This is an absurdly cool video! I have two YouTube accounts and went on both to like this video. Thanks for the great content. You're fantastic at explaining things.

[lookaway]

This just became my favourite youtube channel!

[jessicalearnsthings]

this video was really clear and fun, and i love how excited you get. thanks for this!

[Piipolinoo]

Dude, I saw your video about the skydiving differential equation on reddit and was like "meeeh, not again, we don't need this another time".
But this, this was brilliant! Great video, nice explanation of a scary problem. Keep it up.

Could you also share the jupyter notebooks in the end?
Also, I miss the link to your blog in the video description ;) Keep promoting yourself.

[Ash-ojyv]

This is ridiculously high-quality content

[leonackermann]

Road to Reality in the Background. You know the good stuff ! !

[ewinsart]

Hi Luke, Just a courtesy to let you know that I cited this video in a recent paper. Can't put any details because it gets deleted for containing a link but you can probably find them in your comments box. Great channel!

[stauffap]

Reminds me of the finite difference method that i used once to simulate a 2D Situation with the Navier Stokes Equations.

[Dark-tkxu]

YOU are a great teacher (from a professor).

[aliexpress.official]

that was so cool! saving this.
can you show how to do that for the 3D equation?

Also can you explain the way you wrote the d variable in your code?

[dwipesh]

very interesting. I have one simple doubt about the number of eigen states. The number of eigen states is equal to the dimension of the matrix, and the dimension of the matrix depends on the number of points we have chosen. 

So, the number of eigen states depends on the method of solutions!?

[rajkumarchakraborty]

However you can't use this method for scattering states, as you can't set the boundary conditions as psi(0)=psi(L)=0.

[s.v.]

Really Great Video! Maybe next time you could compare your results with the analytical ones so in this case the qm harmonic oscillator model. I did it and the results are really close! So again thanks for the video

[bigh]

damm looks similar to the euler lagrange equations we studied in aeroelasticity

[pro-bOi]

I was trying to solve woods-saxon potential. I was messed up myself by numerov's algorithm. Then I found your video. Finally I solved the problem using this tridiagonal eigenvalues. But I want to make a request. Can you make a video on how to find all the eigenvalues in a certain range, for any 1-d potential using numerov's algorithm and shooting method.

[moirangthemsanahal]

16:20 aren't energy levels in sho supposed to be equally spaced? In there m and L both are constants so your bar should be increasing linearly right? It seems a little off

[maurocruz]

This is similar to the problem 2.61 of Griffiths 3rd Edition