Edmentum Financial Math Unit5 Activity

Buying stock gives you a share of ownership in the company that issues the stock. Stock investments are risky because stock prices can fall rapidly if the business suffers a loss or if the stock market crashes because of poor economic conditions. So, it’s important to thoroughly research stocks before investing in them.

Let’s say you plan to invest in a company’s stock. Choose a company or brand of your choice. You could think of a product (such as clothes) or a service (such as restaurants) that you use frequently to help guide your selection. Research online to find the information you need to answer the following questions.

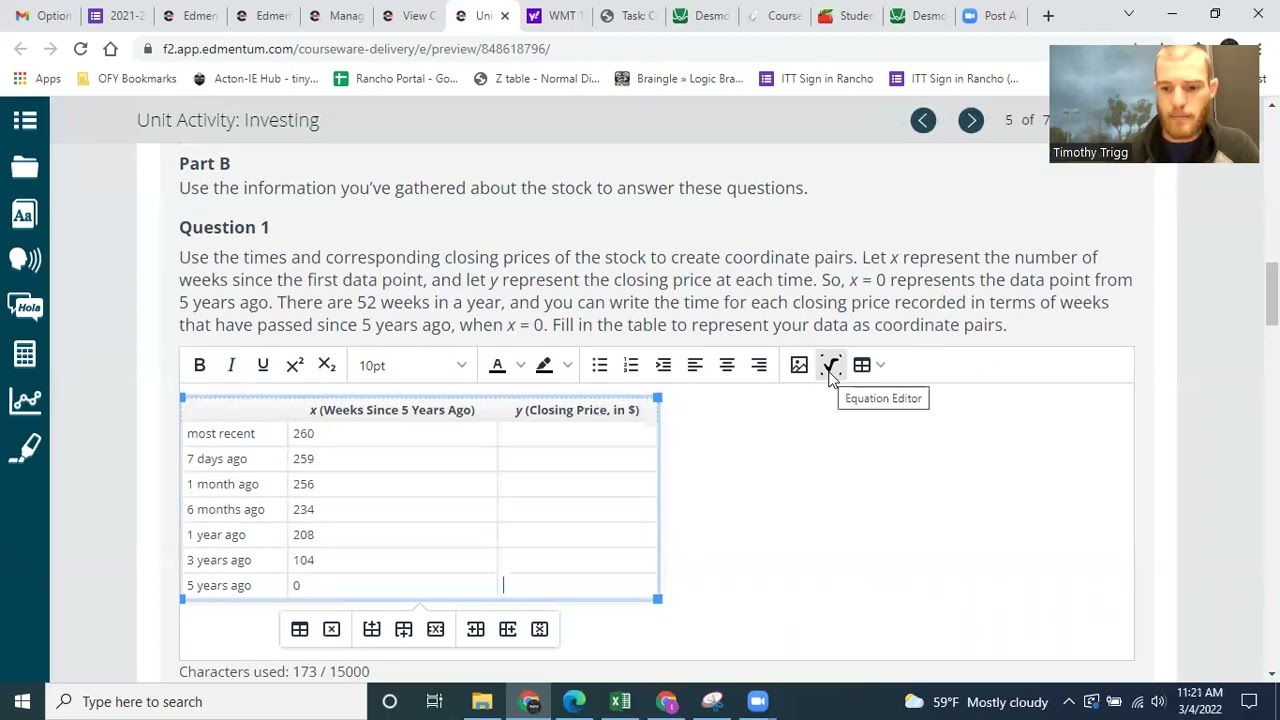
Use the times and corresponding closing prices of the stock to create coordinate pairs. Let x represent the number of weeks since the first data point, and let y represent the closing price at each time. So, x = 0 represents the data point from 5 years ago. There are 52 weeks in a year, and you can write the time for each closing price recorded in terms of weeks that have passed since 5 years ago, when x = 0. Fill in the table to represent your data as coordinate pairs.

Open the graphing tool, and select the data tab. Copy and paste your data from the table (x- and y-coordinates). Don’t include any dollar signs. Plot the data on the graph.

Under the relationship tab, use the linear, exponential, and quadratic function tools with “best fit” selected to view the regression model. Zooming in and out will help you get a better view of each fit. Observe how well each model fits the data. Rank the three function types (linear, exponential, quadratic) in order from best fit to worst fit.

Write two to three sentences justifying your reasoning for the ranking you chose in question 2.

Using a process similar to the one you used in part B, this exponential model was found as the best fit for this data:

y = 30.078(1.003)x.

Use the exponential model to make predictions about closing prices of this stock. Remember that x represents the number of weeks since the first data point, so the value of x today would be 260.

Type the correct answer in each box. If necessary, round the answers to the nearest cent.

Do you think the model is a good predictor of the future closing price of the stock? Justify your response in three to four sentences.

The table lists a variety of investments, along with their purchase cost and a description of their expected gains. Note that because the cost to purchase includes fees, this cost is higher than the initial purchase amount.

Create a diversified portfolio using the information in the table. As you do so, keep these points in mind:

It may be helpful to research any unfamiliar investments to determine their type.
For the pretax expected return, you are computing a simplified estimate because the description of expected gains is an approximation and not an exact prediction.
When computing the pretax expected return for your bond choice, you may find it helpful to refer to the compound interest formula.
Compute the pretax expected returns based on the time frames provided in the description.

Now, use the pretax expected return for your investments and the cost to purchase to find the profit on each investment. Then, find the total portfolio profit.

Which investments in your portfolio, if any, do you consider to be short-term investments? Explain your answer in one to two sentences.

Which investments do you think would be the most profitable to keep long term? Explain your answer in one to two sentences.

Which of the investments are the riskiest, or what should be watched the closest? Explain your answer in one to two sentences.

[bryanna]

you just saved me 😭 i would not have been able to finish this class without this video, thank you so much!

[kkelyn]

Thank you so much! I struggle with fully virtual classes but your channel has helped me lots.

[Mnsterkd]

dude, i was struggling with this assignment for awhile. You help me a lot! thanks!!😭

[aalyyy.]

thank you so much! you made this activity simple and helped me understand what the questions were asking, and how to use the graphing tools they asked us to use. great teacher! thank you

[eternalblessing]

Aye ty for your help! You made it easy and more simple to look at investing.

[dumbb]

these are so helpful thank you so much

[kylabarry]

Hi! Would you be able to do one on Economics Unit 5 Activity: Consumer Economics and Financial Services? This would help a lot!

[yoyonail]

can you make the info tech unit activity 1 plzz