Proof: Recurrence Relation for Bell Numbers (Partitions) | Combinatorics

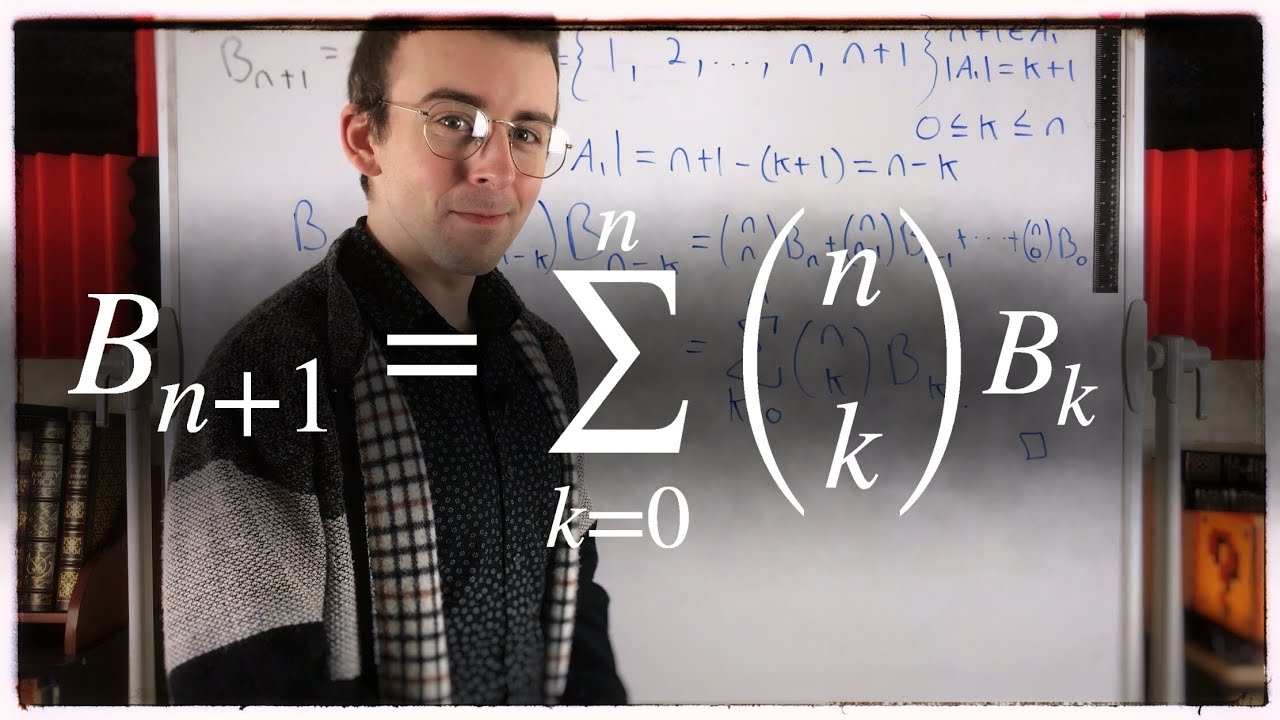
preview_player
Показать описание
We'll be going over a proof of the recurrence relation for the Bell numbers in today's combinatorics lesson. Recall that the bell number Bn is the number of partitions of a set with n objects. By considering an arbitrary partition, and singling out one of its parts, we'll be able to use previous Bell numbers to calculate later Bell numbers with a sum of binomial coefficients multiplied by Bell numbers.

I hope you find this video helpful, and be sure to ask any questions down in the comments!

+WRATH OF MATH+

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Proof: Recurrence Relation 0:13:28

Proof: Recurrence Relation for Bell Numbers (Partitions) | Combinatorics

🔔 Bell Numbers 0:06:44

🔔 Bell Numbers and Its Recurrence Relation (Proof)

Bell Numbers and 0:15:41

Bell Numbers and their Recurrence Relation | Combinatorics

Math 532 - 0:08:13

Math 532 - 7.2 Partition recurrence

Recurrence for partitions 0:03:40

Recurrence for partitions into k parts (visual proof)

Counting Partitions of 0:15:31

Counting Partitions of Sets and Bell Numbers | Combinatorics

Bell Numbers recursive 0:11:25

Bell Numbers recursive relation : Explained with example | dynamic programming tutorial

Exponential Generating Function 0:09:36

Exponential Generating Function for Bell Numbers (Proof)

CO25 A formula 0:27:58

CO25 A formula for Bell Numbers

Proving the Recurrence 0:03:32

Proving the Recurrence Relation of Sterling's Number of Second Kind | Combinatorics | Easy

Checking Solutions to 0:11:50

Checking Solutions to Recurrence Relations (Mathematics for Computer Science)

Math 532 - 0:10:31

Math 532 - 6.2 - Partitions into k parts

Pell Number Lattice 0:03:54

Pell Number Lattice Path Enumeration and visual recurrence formula (synthwave; visual proof)

4.4 Proving closed 0:36:46

4.4 Proving closed forms (FP2 - Chapter 4: Recurrence relations)

Math 532 - 0:07:31

Math 532 - 5.1 Stirling Numbers of the First Kind

L'EXO DE KHÔLLE 0:34:17

L'EXO DE KHÔLLE #15

Recurrence Relation | 0:09:01

Recurrence Relation | Combinatorics Concepts | Math Olympiad | ISI Entrance | TOMATO 55 Sub P2

Roger Penrose explains 0:03:39

Roger Penrose explains Godel's incompleteness theorem in 3 minutes

Terence Tao's Central 0:37:35

Terence Tao's Central Limit Theorem Proof, Double Factorials (!!) and the Moment Method #SoME3

Recurrence Relations: Master 0:15:40

Recurrence Relations: Master Method

L-2.1: What is 0:07:15

L-2.1: What is Recurrence Relation| How to Write Binary Search Recurrence Relation|How we Solve them

Bell numbers #bell 0:00:03

Bell numbers #bell #numbers #shorts #math

Recurrence Relations (1 0:11:38

Recurrence Relations (1 of 3: Introduction & logarithmic example)

Recurrence Relation | 0:13:06

Recurrence Relation | Stirling Numbers of first Kind

Комментарии
Автор

Fantastic demonstration! But I have a question: since we know the recurrence equation for Bn+1 and the value of the first term of Bell number. So Why can't we derive a general equation for each Bell number?

ExploreMath-jnef
Автор

Alas!! I found a treasure, thank you so much for your work. I take Grad combinatorics and you're my life savior lol. Can we have a video about Catalan numbers and their relation with generating functions? Thanks again!!

lalithagurajada
Автор

Thinks sir I understand all concepts very easily.

GauravKumar-qwyf
Автор

sir please share which book you read for bell no.s

ran_domwtf