Terence Tao's Central Limit Theorem Proof, Double Factorials (!!) and the Moment Method #SoME3

==================================================
FOLLOW UP QUESTIONS
==================================================

Possible questions to answer in a follow up videos. Let me know in the comments if you would want to see any of these!

Q: Why is this in a random matrix book? A: There is a similar proof for something called the semi-circle law for random matrices. If you understand this proof, you can understand that one quite easily!

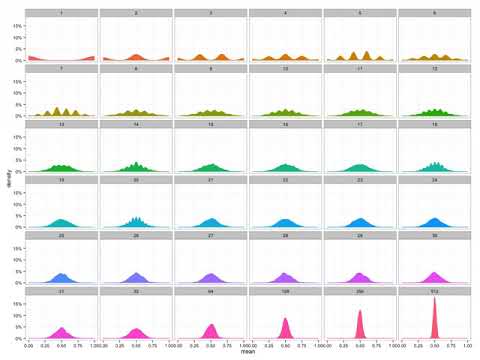
Q: Why is a sum of Gaussian’s still a Gaussian? A: There is a cute way to see this using only moments! It is a cute counting argument with pair partitions which are labeled with some extra labels.

Q: How is this related to the characteristic function/Fourier transform? A: The moments can be added together in a generating series to get things like the characteristic function .

============================================
LINKS
============================================

Link to Terence Tao’s book (from his terrytao blog). The moment method proof is section 2.2.3 starting on page 106.

Short pdf that includes the main proof ideas

3Blue1Brown Central Limit Theorem playlist:

But what is the Central Limit Theorem?

Why π is in the normal distribution (beyond integral tricks)

Convolutions | Why X+Y in probability is a beautiful mess

Why is the "central limit" a normal distribution?

==================================
Info on how the video was made
==================================

===============
Timestamps
===============

0:00 Terence Tao
0:38 What is the CLT
2:40 But why?
3:30 Double factorials
4:30 Gaussian moments
5:52 Moments of sums
6:29 Pair partitions
9:00 Two main results
10:08 Part 1-Gaussian moments
13:08 Solving the recurrence relation
15:35 Part 2-Moments of sums
17:17 k equals 1
18:00 k equals 2
21:47 k equals 3
25:42 k equals 4
29:41 Recap and overview

#3blue1brown #some #some3 #probability #Gaussian #math #integration #integrationbyparts #combinatorics

[diribigal]

I made it. Also, I was all ready to ask about Moment Convergence but you addressed it very well at the end. Great video showing the beautiful recursion here!

[diffusegd]

If you're wondering about the "Random matrix" theory mentioned somewhere,

Normally when we consider random variables, they are real/complez valued. In particular, they are *Commutative*. XY is distributed the same as YX

In the case of random matrices, since matrices themselves aren't commutative, random matrices aren't either. This causes problems with usual independence properties. For example, for two Gaussian Unitary ensembles (a common random matrix), E(XYXY) != E(XXYY)

(I just used the expectation of a random matrix here. This is defined as the expected value of the eigenvalues.)

It turns out, when you have Non commutative random variables, there exists a central limit theorem!
But it is not a normal distribution. It is a semicircular distribution!

The proof follows the same way as the video, except when we have partitions, we instead have only the *non-crossing partitions*. It turns out the number of non-crossing partitions is the Catalan numbers, which also happen to be the moments of the Semicircle distribution!

And lastly, remember the Gaussian ensembles before? It turns out as the matrix size goes to infinity, the eigenvalues are semicircular distributed.

[kikivoorburg]

I made it through the proofs! I really appreciated that you laid out the direction we were going before actually proving each step - giving an overview beforehand makes it much clearer what we’re doing and why. Great job!

[rnengy]

I made it through to the end! As a physicist, the connection between pairing objects and Gaussian moments reminds me of Wick’s theorem. I had heard that quantum field theory and random matrix theory were related, and this just looks like the start of the rabbit hole — excited to see where this leads in future videos!

[MihaiNicaMath]

I have a few ideas for follow up videos related to this video (subscribe if you are interested!). Let me know which of these three question you most would like to see an answer to (or let me know if you have other questions that would make a good follow up!)

Q1: Why is this in a random matrix book? A: There is a similar proof for something called the semi-circle law for random matrices. If you understand this proof, you can understand that one quite easily! This topic is a great introduction into the wonderful world of random matrices.

Q2: Why is a sum of Gaussian’s still a Gaussian? A: There is a cute way to see this using only moments! It is a cute counting argument with pair partitions which are labeled with some extra labels.

Q3: How is this related to the characteristic function/Fourier transform? A: The moments can be added together in a generating function to get things like the characteristic function .

[Qsdd]

This is pretty well-suited for someone at an undergrad level who has taken a solid probability course and remembers their partial integration. You sweep a little bit under the rug with the latter but I think we all survive. Being just a teensy bit more clear about E(X^0)=1 (that this is just the total probability) might be good for that level. Also maybe some comments about how we may reduce to the case of mean 0 and variance 1 would be good.

[thefunpolice]

A nice exposition. Made it to the end and enjoyed every moment.

The CLT completely blew me away when I first heard of it, it made statistical analysis, which I had foolishly disregarded as a bit wishy washy, suddenly seem beautiful and curious.

From memory there's a nice description of the convolution proof of the CLT in Brad Osgood's excellent lectures on Fourier Methods (available on YouTube) for anyone who is interested in seeing that.

[columbusmyhw]

I really like how you "cut through the curtain" at the start and end and show us a more rough presentation. It allows for more off-the-cuff remarks that don't necessarily "fit" into a tightly scripted video.

[joshdavis]

As a mathematician who is also currently taking mathematical probability and probability, this video is just what I have been needing! Thank you, good sir.

[surojitbiswas]

ONE OF THE BEST VIDEO ON CLT. NICELY EXPLAINED, THANK YOU.

[mirkoserino]

Amazing, the clearest proof of the CLT I have ever come across !

[davids]

Nice Proof. I think the result that the k-th moment of the Sum of Variables is the number of pairings is interesting in its own right. That was an eye opener.

[rafaelschipiura]

Very nice video, it was exactly what I was looking for to go with my prob course. You talk about calculating probabilities of series in the end, but in practice for any n > 4, the Normal distribution is already pretty good, so it can be used for most summations, not just for a series. Talk about a small infinity. So I would love to see a video on not taking n to infinity, but about how fast does the two random variables approach each other.

[Mutual_Information]

4:50 whoa.. I never knew this!

And btw, just discovered your channel - it's top tier! Instant subscribe

[stanleydodds]

The moment convergence proof of CLT (or proof outline, with rough details of moment convergence implying convergence in distribution) is what we were shown in school, probably because as mentioned it's the most elementary way to prove it, so it was easy to get through in one lesson. I'm sure I also saw further proofs of CLT at university (I know there are some ways to relax the conditions needed for the theorem to apply to a distribution), but I've definitely forgotten any details about those by now, so the moment convergence is always my go-to way to demonstrate it.

[sdsa]

unlike convolutions, the most striking aspects of this video for me are pair partitions and singletons and their notation for proving central limit theorem.... there are a lot of useful math tricks ... I am going to watch it again to learn them all! Thank you!

[jacoboribilik]

Great video. I like this CLT version is valid for sequences of idependent r.vs not necessarily identically distributed. One would generally prove Lindeberg's and Lyapunov's versions to deal with non identically distributed r.vs

[theodorevassilakis]

Made it to the end and really appreciated the high quality presentation. I’d be interested to see your list of most impactful applications of CLT, whether in data science / computing or other areas of math.

[kdpwil]

Great video! My only comment is that @27:44 in the video you state that the nE[x_i^4] term goes to zero when you normalize by square root of n. I didn't catch that when you normalize by the square root that you simultaneously raise the square root to the fourth power in the denominator. I had the impression that you were saying that the limit as n goes to infinity of the quantity nE[x_i^4]/sqrt(n) was zero when it clearly goes to infinity. You very nicely corrected this impression at @29:09.

[colinbackhurst]

I'm here as a SoME3 reviewer. An interesting subject and a good video. Oh and I made it to the end of the proof ;-)