One Parameter Family of Hamiltonian Systems

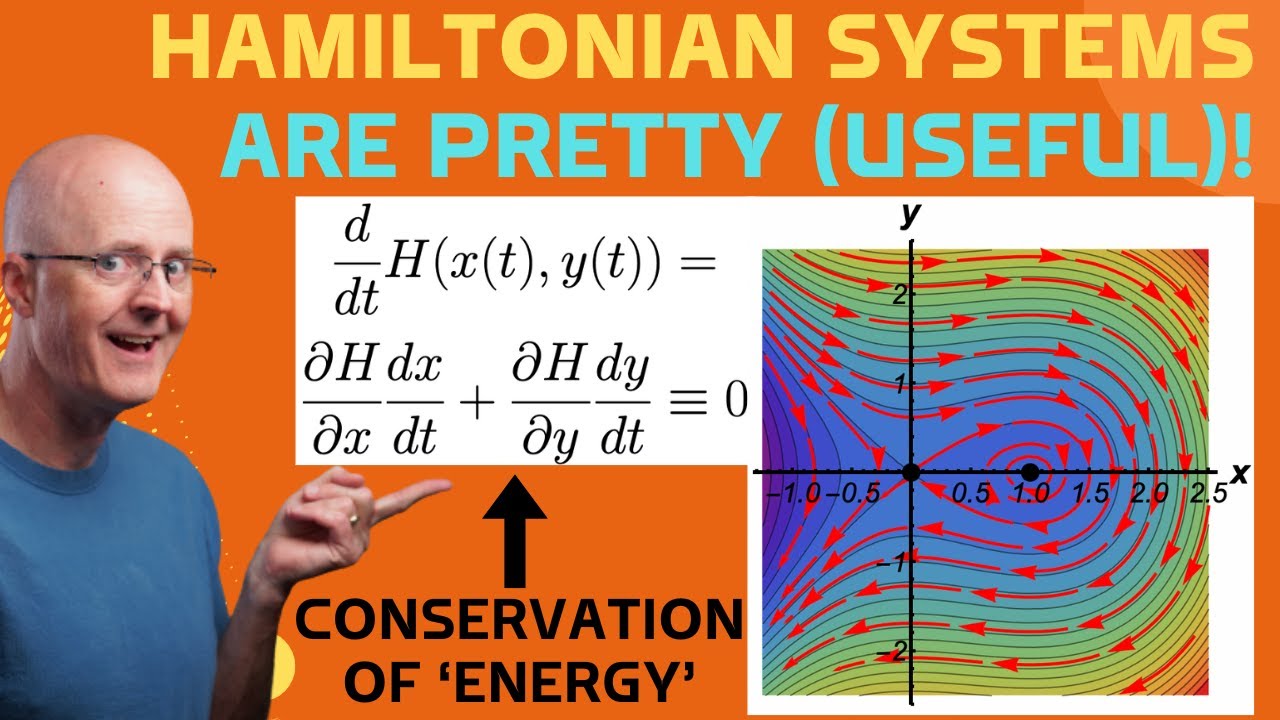
The one-parameter family of nonlinear systems dx/dt = f(x,y) = y, dy/dt = g(x,y) = x - x^2 - a is a Hamiltonian system. We can check this by confirming that ∂f/∂x = -∂g/∂y, which is a necessary condition for the existence of a Hamiltonian function by Clairaut's Theorem about the equality of mixed second order partial derivatives. It is also sufficient. The Hamiltonian function H is found by two integrations. The Hamiltonian function is constant along solution curves by the Chain Rule from Multivariable Calculus. Then we use ContourPlot in Wolfram Mathematica to draw the level curves of H and StreamPlot to sketch solutions in the vector field (f,g). The corresponding gradient system and Liapunov functions are briefly discussed.

Links and resources
===============================

AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.