The Hamiltonian Flow

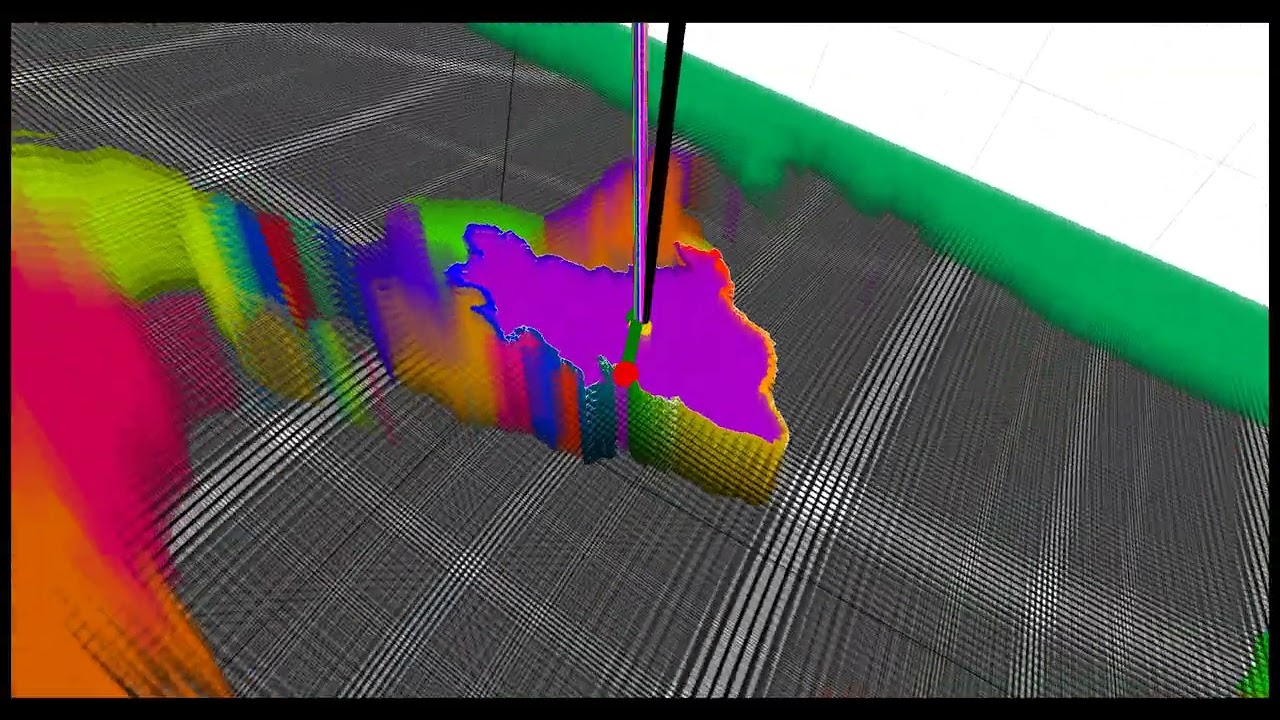
The set of equally spaced parallel planes is called a stack. The positive direction agrees with the motion of a falling particle in the gravitational field of the Earth. The stack represents the gravitational work 1-form and its direction is downward. A golden particle travels in the direction of the black arrow. Over the first few seconds of falling towards the Earth’s center, the traveling distance is short. That is why the spacing is approximately constant between every parallel plane in the stack. The 1-form of the motion vector equals the sum of planes pierced by the vector. The greater the value of work 1-form, the higher the density of stack planes. It is equivalent to the work done moving the particle mass along the vector. The magnitude of the gravitational field (the gravitational constant) for a mass near the surface of the Earth is equal to the inverse of the spacing between planes. See figures 32.2,3 in Tristan Needham 2021.

The Hamiltonian flow is a vector field on phase space. Given initial position and momentum, the Newtonian time-evolution of the falling particle is shown using arrows on the cotangent bundle of configuration space. Per unit mass, the Hamiltonian equals the squared norm of particle’s momentum over two, plus the gravitational constant times the norm of particle’s position. Given a momentum initialization, the Hamiltonian values are fixed for all positions in a plane. The potential energy is the same everywhere in a plane in the stack, and is proportional to the norm of position, which is the radius of the Earth plus the height of the particle from the Earth’s surface. As the particle falls freely, follows a geodesic trajectory in the configuration space, as if gravity is removed. Then the total energy of the dynamical system is conserved to make the derivative of the Hamiltonian with respect to time equal to zero. Falling to the Earth, the particle must gain as much kinetic energy (momentum) as it loses in potential energy (height). See figure 20-5 in Roger Penrose 2005.