Newton's Law of Cooling... Applying Differential Equations [Real World Calculus!]

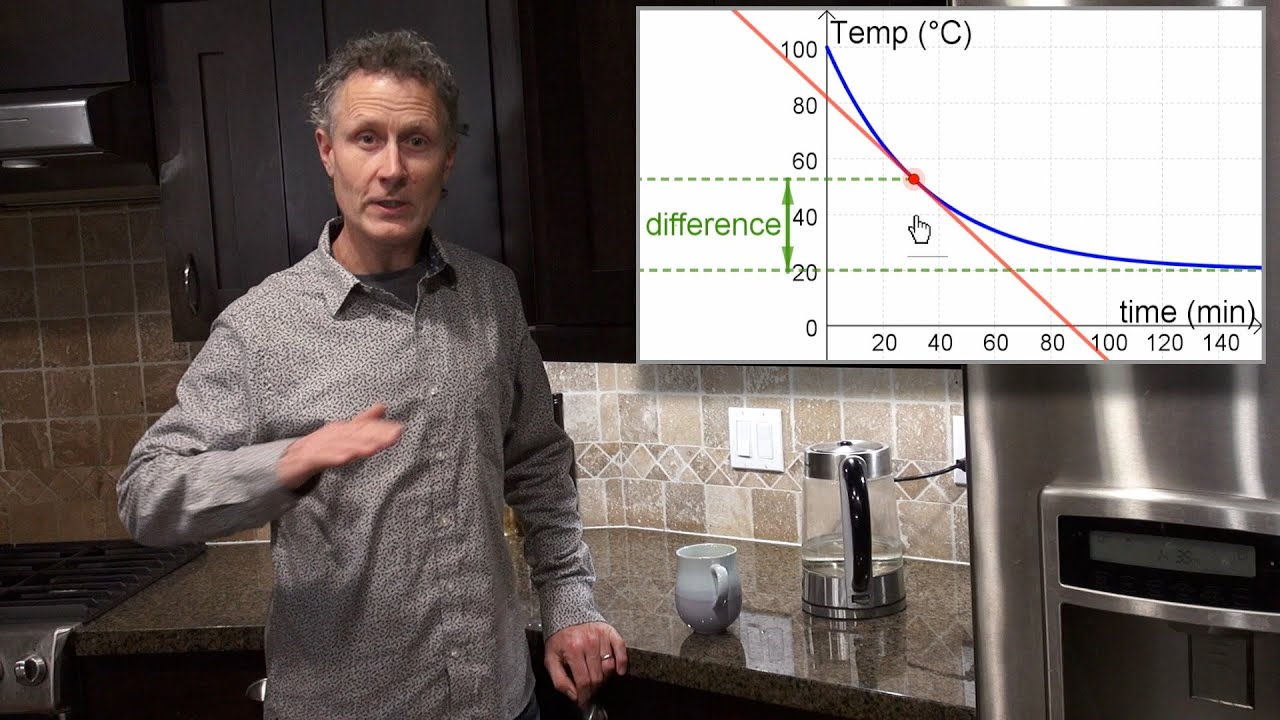
Looking for Calculus in real world situations? Here differential equations are used to represent Newton's Law of Cooling and solve several related problems, in a similar way to other situations involving the rate of change of a quantity being proportional to that quantity.
My instructional approach emphasizes conceptual understanding of and connections between concepts and ideas, rather than just pure memorization.

#SituationalMathVideos #APCalculusbytheAAMG #AllAroundMathGuy

[tww]

The graph is very helpful, particularly the dynamic part. 0:51 It finally clicked! As the difference in (T) and (ambient T) gets smaller, the slope of the tangent line gets smaller ( approaches 0), which corresponds to a smaller rate of change ( dT/dt).