filmov
tv
Discrete Math - 2.3.3 Inverse Functions and Composition of Functions

Показать описание
Practice with inverse and composition of functions.
Video Chapters:
Introduction 0:00
Inverse Functions 0:06
Show a Function is Invertible and Find the Inverse 1:57
Composition of Functions 6:46
Composition Practice 8:12
Up Next 11:43
Textbook: Rosen, Discrete Mathematics and Its Applications, 7e
Video Chapters:
Introduction 0:00
Inverse Functions 0:06
Show a Function is Invertible and Find the Inverse 1:57
Composition of Functions 6:46
Composition Practice 8:12
Up Next 11:43
Textbook: Rosen, Discrete Mathematics and Its Applications, 7e
Discrete Math - 2.3.3 Inverse Functions and Composition of Functions
Discrete Math 2.3.3 Inverse Functions and Composition of Functions
Composition of relations | MISTAKE - explained RoS instead of SoR and vice versa | otherwise correct
[Discrete Mathematics] Inverse Function Examples
How To Find The Inverse of a Function
Composition of Relation with Itself
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Inverse of a 3x3 Matrix
Mathematics 3 DBATU Lonere for All Branch Engineering 3rd Sem 2nd Year Syllabus & Class Announce...
Composition of Function Problem 2 and 3 - Functions - Discrete Mathematics
6÷2(1+2)=???
Check if f(x)=4x+3 is invertible then find inverse of f
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Function (composite and inverse)
Inverse of a Function | Invertible Function | Discrete Mathematics
How To Find The Inverse of a Number ( mod n ) - Inverses of Modular Arithmetic - Example
Converse, Contrapositive and Inverse
Proof and Problem Solving - Relations Example 01
Discrete Math - 2.3.2 One-to-One and Onto Functions
Relation and Function: How to Find Inverse of a Function #1
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Composite and Inverse Functions | Discrete Mathematics Lecture 9 | By Gp sir
Composite Functions
Multiplication of Matrices Class 9
Комментарии
 0:12:02
0:12:02
 0:09:48
0:09:48
 0:03:20
0:03:20
![[Discrete Mathematics] Inverse](https://i.ytimg.com/vi/1cvQhfZGF7Q/hqdefault.jpg) 0:06:01
0:06:01
 0:11:36
0:11:36
 0:06:59
0:06:59
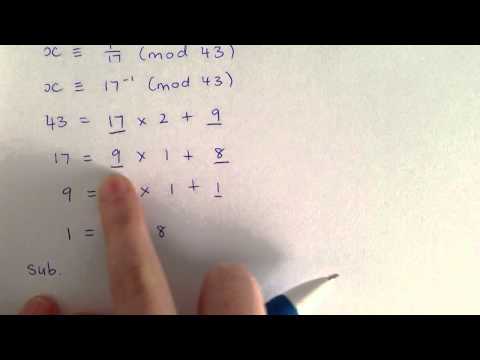 0:06:00
0:06:00
 0:15:21
0:15:21
 0:10:29
0:10:29
 0:06:41
0:06:41
 0:01:21
0:01:21
 0:04:58
0:04:58
 0:05:45
0:05:45
 0:16:06
0:16:06
 0:08:42
0:08:42
 0:10:58
0:10:58
 0:03:47
0:03:47
 0:08:57
0:08:57
 0:10:58
0:10:58
 0:06:11
0:06:11
 0:00:16
0:00:16
 0:19:39
0:19:39
 0:05:23
0:05:23
 0:00:33
0:00:33