Infinite Geometric Series & Intro to Limits in Calculus - Part 1 - [18]

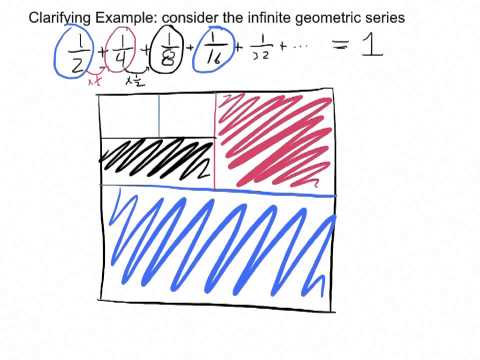
In this lesson, you will learn how to write down the terms of a geometric series. A geometric series consists of the sum of the terms in a geometric sequence, where each successive term is found by taking the previous term and multiplying by a common ratio. If we have a geometric series that has an infinite number of terms, we say that it is an infinite geometric series. Even though this type of series has an infinite number of terms, the sum of these terms approaches a finite number, called the limit, and we say that series converges. The infinite geometric series converges if the common ratio is less than 1. In this lesson, we will explain how infinite geometric series work, how to calculate the sum of an infinite number of terms, and introduce the concept of a limit in calculus. Limits form the foundation of all of calculus.

[NidhiSinhaU]

You are such an awesome teacher Jason Gibson. If there was a Nobel Prize for teaching, you would have been winning that one every year

[stevenmoreno]

Hello Mr. Gibson,

I just wanted to take this chance to thank you for helping me in many subjects like chemistry.
I am good at chemistry, but you were always a second address if I had to know something for school.
Thanks to you help I am very successful in school, that's the reason I'm writing this comment.
Greetings from Germany

[andij]

thanks so much. i'm re-learning high school maths, plus want to learn some new stuff, your channel is awesome, i love the pacing of the lessons in addition to the content itself

[hemarajue]

Already I learnt this geometric series from one of your lessons. One point I cleared from this lesson is the range of common ratio.
Success is neither a minute work nor a day long work. Rather, it's how much time you spend in a day to reach your goal.

[jessesmith]

Oh my gosh I probably watched like 10 different videos explaining the same topic and I couldn’t understand anything but just watching your video to the 6 minute mark made everything so clear now. THANK YOU. You have a talent for simplification!

[fahimkhalasi]

I like your video on infinite geometric series because it has lots of applications to calculus, limits and beyond.

[rrrbb]

I have been looking at divergent series for a while, and think statements like "-1 = 1 + 2 + 4 + 8 + ... " are just badly stated, but not actually wrong. What's wrong is that in the " + ... " you are not told what is in the tail. If you use recursion, it is concrete, and you can just do the algebra; and never resort to appeals to infinity in any way.

T = Sum(T, n) + Tail(T, n).
T = 1 + 10 T.
(1-10)T = 1.
-9 T = 1.
T = -1/9. ??? because common ratio is 10... but carry on....

T = (1 + 10 T)
= (1 + 10 (1 + 10 T))
= (1 + 10 + 100 T)
= (10^0 + 10^1 + 10^2 + ... + 10^n) + 10^{n+1} T
= Sum(T, n) + Tail(T, n).

T is -1/9, yet it expands like: "1 + 10 + 100 + ... ".

But notice that we dropped the recursive tail, because we don't believe in its importance. T is only Sum(T, n) when Tail(T, n) goes to zero. So, T doesn't mean what people think it does. But T is meaningful. It's a number required to calculate the closed form of the sum of n terms.

T -Tail(T, n) = Sum(T, n)
T(1 - 10^{n+1}) = Sum(T, n)
(-1/9)(1 - 10^{n+1}) = Sum(T, n)
(10^{n+1}-1)/9 = Sum(T, n)

This takes the mystery out of divergent series being associated with a number. The sum is not T. It's Sum(T, n), which is equal to T-Tail(T, n). Recursion might be the only really concrete way to specify infinite processes; because it still uses finite iteration.

When you have a series where there's not a common ratio, but it goes up by 1 for a coefficient, you can usually get there by differentiating a series like this one; so you can do term-by-term addition of series. Because of this, you don't run into any of the odd issues of commutativity/associativity that you will get when infinity is explicitly involved. Recursion is a much more sound basis, when you have a way to use it.

You will run into this problem pretty early on if you try to automate computer algebra. If you follow the algebraic rules and both expand a sequence to a sequence, and also solve it for a number; a computer has no good way to object to it. All you can do is to change the algebra rules until they give you what you want, without breaking unrelated things. So, you have to face this issue of divergent series. It almost always means that we are interpreting it wrongly

The fact that you end up subtracting the tail off of an "infinite" sum to recover a finite sum up to n terms says something deep about infinite processes. It says to me that the concept of an infinite process is kind of hand-wavy, when compared to algebraic rules that you follow without objecting to the results; where you sometimes need to carefully re-interpret something that doesn't make sense.

If S is not the sum here when it's true for EVERY value of n, including the largest one...

S = Sum(S, n) + Tail(S, n)

and S is an actual value, but Sum(S, n) is large-positive and Tail(S, n) is large negative; then that means that we are misinterpreting what S even is. S-Tail(S, n) = Sum(S, n) is unbounded. But S is a constant. And as n->inf, Tail(S, n) doesn't go to zero, then you can't say that S = Sum(S, n) at all. It's just that we can confuse the two when -1 < r < 1, S = Sum(S).

Note where you get a square wave of 0, 1 values:

A = 1 - A.
(1+1)A = 1.
A = 1/2.

// written without a tail, it's nonsense.
A = (-1)^0 + (-1)^1 + (-1)^2 + ...
= 1 - 1 + 1 - 1 + ...

A isn't the sum. A-Tail(A, n) is the sum. Sum(A, n) oscillates between 0 and 1. Yet A has a value, and it's 1/2. A has to have a value, to be true no matter how many times you expand the recursion. And if you expand to a particular pattern through recursion, then you are equal to that infinite sequence; though different sequences can be equal to the same number.

[nyambemukena]

Sir you are out a wonderful teacher, you are helping me a lot. This question is troubling me, please help me sir, the sum to infinity is equal to 36 and the sum of the first three terms of a Geometric progression is 81/2, find the first three terms.

[chun-techou]

Does the sum of the geometric series is still equals to 1 if the common ratio is a negative fraction?

[eslamelsofany]

thanks a lot mr. jason
can you inform us your courses plan for this year ?

[ZawZaw-olvc]

Do you have calculus course on YouTube ?

I think this is the topic on which Ramanujan worked extensively