filmov
tv
Une technique ROYALE de calcul intégral

Показать описание
Vidéo présentant une technique de calcul intégral formidable qui saura vous surprendre j'espère ! Elle me tenait particulièrement à coeur. La vidéo est plus courte que d'habitude, n'hésitez pas à me dire si le format vous plaît !
Lâche un com' si tu le souhaites ! C'est important d'avoir des retours.
Pour tout contact Instagram est à privilégier, je suis sûr de voir tout type de requête sans que vous ne soyez noyé dans les commentaires dont les notifications ne me parviennent pas nécessairement !
Lâche un com' si tu le souhaites ! C'est important d'avoir des retours.
Pour tout contact Instagram est à privilégier, je suis sûr de voir tout type de requête sans que vous ne soyez noyé dans les commentaires dont les notifications ne me parviennent pas nécessairement !
Une technique ROYALE de calcul intégral
Une intégrale SPECTACULAIRE
Calculer une intégrale (1) -Terminale
Ne JAMAIS partir SANS SA COPINE 🫢 #humour #blague #drole #couplegoals #internationalcouple #shorts...
Quand LA PROF te CLASH devant TOUTE LA CLASSE #animation #mdr #humour #clash #cartoon #lol #fun
Voici Pourquoi Vous Ne Devez Jamais Faire De Piercing !😱
😱 Silure Géant 🎣 #fishing #fish #silure
Méthodes de calcul rapide
j'ai tout les preuve a propos de Zizou et ania 😭😭
CETTE ILLUSION VA VOUS FAIRE OUBLIER VOTRE NOM #youtubeshorts #youtube #illusion #shorts
JE JÈTE SA MANETTE DU 6 ÈME ÉTAGE 😱😂
LES MAUVAISES NOTES L’ÉCOLE/COLLÈGE/LYCÉE…
J'étais pas prêt 😱
Voici Comment Enlever Un Tique
astuces sur les graphes : mathématiques
Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...
Elle m’a dit « non » à la mairie ! 😂 #mariage #shorts #short
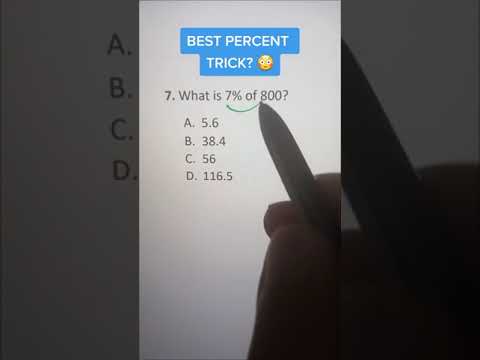
How To Calculate Percents In 5 Seconds
NEWYES Calculator VS Casio calculator
Le MEILLEUR BUG pour MONTER en RANK sur FORTNITE 🤣💀
Quand tu peux seulement prendre UNE cuillère..
Little Girl Answering Abacus Questions🧮#makeyourchildageniuswithlubna #study #Abacus #shorts
If you read class 7 now then you look at page 154 of maths book what is it ?😳💀📃📄📖📚🖕🏻...
🎃Maquillage halloween🎃 Effet Spécial Trou Dans La Main 😦
Комментарии
 0:11:28
0:11:28
 0:09:21
0:09:21
 0:03:46
0:03:46
 0:00:16
0:00:16
 0:00:13
0:00:13
 0:00:27
0:00:27
 0:00:17
0:00:17
 0:02:49
0:02:49
 0:00:28
0:00:28
 0:00:44
0:00:44
 0:00:24
0:00:24
 0:00:11
0:00:11
 0:00:11
0:00:11
 0:00:28
0:00:28
 0:00:22
0:00:22
 0:00:13
0:00:13
 0:00:28
0:00:28
 0:00:08
0:00:08
 0:00:14
0:00:14
 0:00:44
0:00:44
 0:00:31
0:00:31
 0:00:18
0:00:18
 0:00:08
0:00:08
 0:00:42
0:00:42