Static equilibrium minimum angle for the ladder problem. Rod leaning against wall minimum angle.

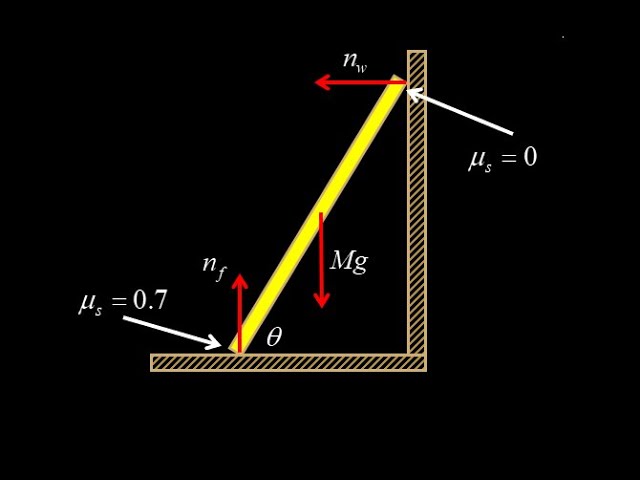
Classic static equilibrium problem called "static equilibrium minimum angle for the ladder problem", "static equilibrium beam against wall" or "static equilibrium ladder against wall" etc. For the board leaning against wall, minimum angle is computed before the beam or ladder breaks loose due to overwhelming the static friction force at the contact point with the ground.

Static equilibrium ladder against the wall problem using torque and force analysis:

In this slipping ladder problem, given the coefficient of static friction at the floor, we compute the minimum angle before the ladder or beam will slip (we assume the wall is smooth). It takes some trigonometry work to compute all the angles between the forces and the lever arm, then we analyze torque about the contact point with the ground, horizontal forces and vertical forces to get a system of three equations. Finally, we are able to solve for the minimum angle before slipping in general and plug numbers in to get the Rod leaning against wall minimum angle.

[seth-langendoen]

I had a question very similar to this one and it really helped me understand all of the concepts to specific moments thanks!

[furkanyerli]

what happened if there was a friction at the wall

[nilmeiarmenta]

Easy to understand but the way you right ta letters can't identity it clearly. Thanks!

[unknown-sons]

A 30ft ladder weighing 100 lb having its center of the mass one-third of the way up  from the bottom rests against a smooth wall so that it makes an angle of 600" class="Wirisformula" role="math" alt="60 to the power of 0" style="box-sizing: border-box; vertical-align: -4px; border-style: none; height: 22px; width: 26px;"> with the ground. If the coefficient of friction between the ground and the ladder is 0.4, how high can a 150-lb man go before the ladder slips?