filmov
tv
Limit Duality Theorem
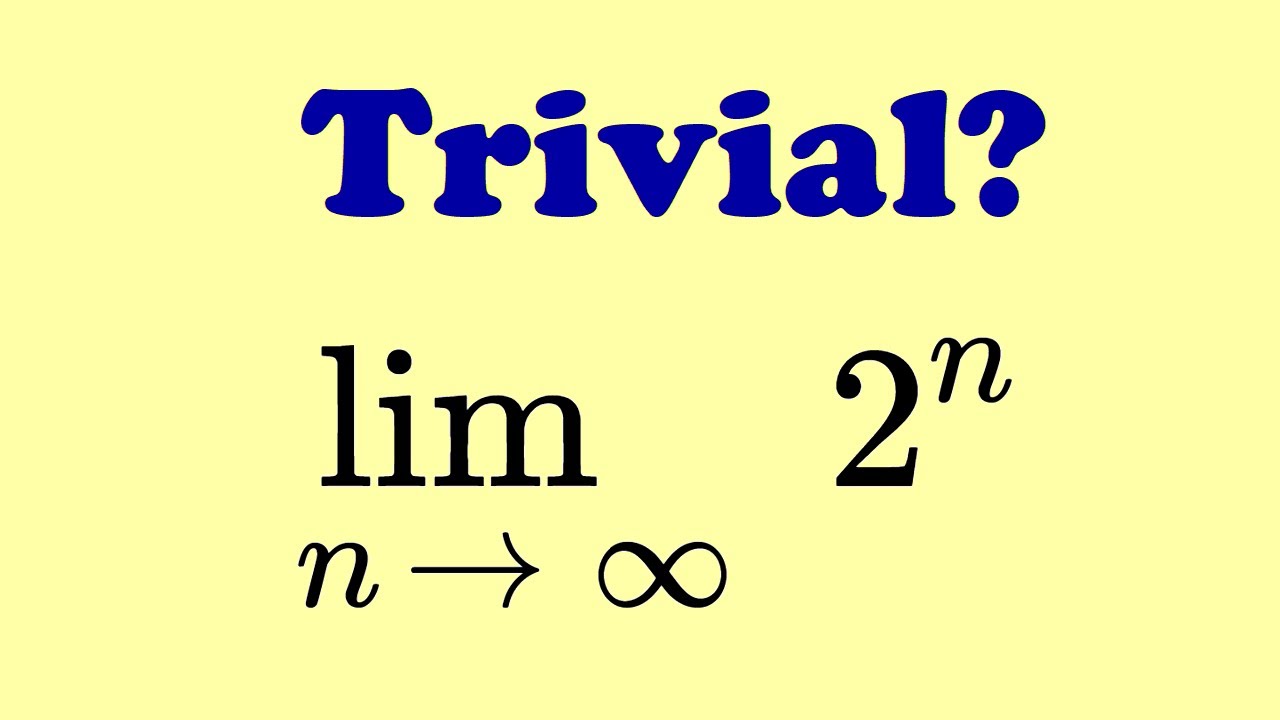
Показать описание
Duality Theorem
In this video, I use a neat little trick to show that the limit as n goes to infinity of 2^n is infinity, by using the fact (shown before) that the limit of (1/2)^n is 0.
Other examples of limits can be seen in the playlist below.
In this video, I use a neat little trick to show that the limit as n goes to infinity of 2^n is infinity, by using the fact (shown before) that the limit of (1/2)^n is 0.
Other examples of limits can be seen in the playlist below.
Limit Duality Theorem
Duality Problem 1,2 - Linear Programming Problems (LPP) - Engineering Mathematics - 4
Limits and Adjoints in Category theory ; Stone duality in propositional logic
V4-07. Linear Programming. The Duality Theorem.
Duality theorems
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
The Duality Theorem
[OR3-Theory] Lecture 2: Duality #5 Weak duality and sufficiency of optimality
Quantum 101 Episode 1: Wave Particle Duality Explained
Weak Duality Theorem | Proof in 4 lines
CSE 550 (2022, Fall): 3.3 Maximum-Flow LP and Duality
Duality: Lagrangian and dual problem
Copy of Lecture 8 (part 2): Duality Theory in Linear Programming
Duality of Max Flow - Georgia Tech - Computability, Complexity, Theory: Computability
Lagrangian Duality and Weak Duality Theorem
Theorems on Duality | Fundamental Duality Theorems | Existence Theorems | Complementary slackness
Linear Programming, Lecture 16. More examples on dual problems. Duality Theorem.
Easiest Way to Write the Dual of LPP - A Short Cut trick
If you do timepass then professor do this😂🤣 at IITBOMBAY,#iitbombay
A Primal-dual Analysis of Margin Maximization by Steepest Descent Methods
Horatiu S. Nastase - Probing holographic dualities through Penrose limits and dual spin chains
V4-10. Linear Programming. The Duality Theorem. part 4.
'Deriving Gauge-String Duality' by Prof. Rajesh Gopakumar (ICTS, Bangalore)
Комментарии
 0:07:01
0:07:01
 0:07:32
0:07:32
 3:31:42
3:31:42
 0:13:34
0:13:34
 0:18:23
0:18:23
 0:00:19
0:00:19
 0:00:16
0:00:16
 0:25:19
0:25:19
![[OR3-Theory] Lecture 2:](https://i.ytimg.com/vi/ugXcLSK-cXQ/hqdefault.jpg) 0:07:49
0:07:49
 0:03:32
0:03:32
 0:09:30
0:09:30
 0:17:39
0:17:39
 0:13:50
0:13:50
 0:47:58
0:47:58
 0:02:08
0:02:08
 0:14:16
0:14:16
 0:00:40
0:00:40
 1:12:53
1:12:53
 0:16:20
0:16:20
 0:00:31
0:00:31
 0:41:42
0:41:42
 0:31:25
0:31:25
 0:16:44
0:16:44
 1:27:53
1:27:53