filmov
tv
Complex Analysis 31 | Application of the Identity Theorem
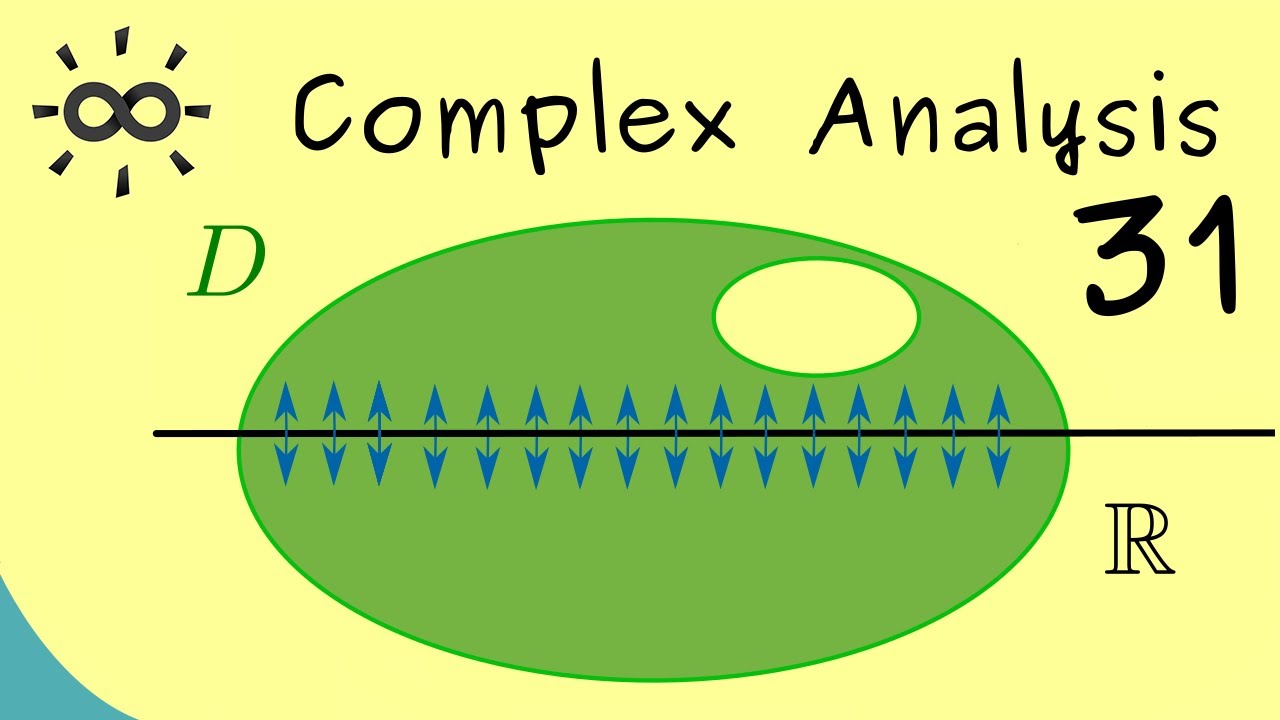
Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
Thanks to all supporters who made this video possible! They are mentioned in the credits of the video :)
This is my video series about Complex Analysis. I hope that it will help everyone who wants to learn about complex derivatives, curve integrals, and the residue theorem. Complex Analysis has a lof applications in other parts of mathematics and in physics.
This is the last video in the Complex Analysis Series.
#ComplexAnalysis
#Analysis
#Calculus
#Mathematics
#curveintegral
#integration
(This explanation fits to lectures for students in their first or second year of study: Mathematics, Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Complex Analysis 31 | Application of the Identity Theorem
Complex Analysis 31 - Contour Integral
complex analysis 31
Complex analysis - 31 Problems on orthogonal trajectory of the family of curves
Complex Analysis 31 - Winding number, Argument Principle and Rouches Theorem
Complex Analysis and physical applications
Complex Analysis - 31: Isolated Singularities - 3
Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6
CUET PG 2025 MSc Maths | Complex Analysis | Free Class | CUET MSc Maths 2025 | Akash Sir
Complex Analysis, GATE 2003 Question (Q.ID.M(GATE)CA31)
Intro Complex Analysis, Lec 31, Laurent Series, Poles of Complex Functions, Essential Singularities
The Beauty of Complex Numbers in 'Visual Complex Analysis', by Tristan Needham (& Math...
Complex Analysis - Computing Line Integrals
Complex Analysis : - ( Algebraic numbers ) - 31.
Complex Analysis, GATE 2003 Question (Q.ID.M(GATE)CA31)
Complex Analysis
Conformal Mapping | Möbius Transformation | Complex Analysis #25
How to eat Roti #SSB #SSB Preparation #Defence #Army #Best Defence Academy #OLQ
Complex Analysis : - ( Representing the complex number in complex plane ) - 31.
Complex Analysis 1 by Dennis G Zill Solutions||lec#31||Ch#1||Ex#1.1||Q#31 & 32|| #complexanalysi...
Complex Analysis 10 | Uniform Convergence
Complex Analysis Part 31
Complex Analysis 30 | Identity Theorem
Lec-31 | Cauchy's Residue theorem & its application | Complex Analysis | Nayan Sir
Комментарии
 0:06:11
0:06:11
 0:09:36
0:09:36
 0:35:48
0:35:48
 0:19:27
0:19:27
 0:43:30
0:43:30
 0:45:31
0:45:31
 0:42:37
0:42:37
 0:40:45
0:40:45
 0:57:45
0:57:45
 0:06:41
0:06:41
 0:55:30
0:55:30
 0:06:37
0:06:37
 0:07:03
0:07:03
 0:09:53
0:09:53
 0:06:18
0:06:18
 0:03:25
0:03:25
 0:25:42
0:25:42
 0:00:16
0:00:16
 0:12:11
0:12:11
 0:02:53
0:02:53
 0:07:11
0:07:11
 0:05:41
0:05:41
 0:16:02
0:16:02
 0:23:31
0:23:31