filmov
tv
Oxford Calculus: Heat Equation Derivation

Показать описание
University of Oxford mathematician Dr Tom Crawford derives the Heat Equation from physical principles. The Heat Equation is one of the first PDEs studied as an undergraduate maths student.
We start with a one-dimensional long and thin cylindrical rod which has heat flowing through it from left to right. We calculate the change in the internal energy for a short section between x=a and a+h (for small h) using Liebniz Rule. This must be equal to the heat flux in minus the heat flux out of the segment.
By dividing both sides of the equation by h and taking the limit as h tends to zero we arrive at the first equation relating the temperature to the heat flux. We then use Fourier’s Law which relates the heat flux to the temperature gradient to rewrite the equation in terms of only the temperature. Finally, the extension of the equation to 2D and 3D is discussed.
Check your working using the Maple Calculator App – available for free on Google Play and the App Store.
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
We start with a one-dimensional long and thin cylindrical rod which has heat flowing through it from left to right. We calculate the change in the internal energy for a short section between x=a and a+h (for small h) using Liebniz Rule. This must be equal to the heat flux in minus the heat flux out of the segment.
By dividing both sides of the equation by h and taking the limit as h tends to zero we arrive at the first equation relating the temperature to the heat flux. We then use Fourier’s Law which relates the heat flux to the temperature gradient to rewrite the equation in terms of only the temperature. Finally, the extension of the equation to 2D and 3D is discussed.
Check your working using the Maple Calculator App – available for free on Google Play and the App Store.
You can also follow Tom on Facebook, Twitter and Instagram @tomrocksmaths.
Get your Tom Rocks Maths merchandise here:
Комментарии
 0:25:20
0:25:20
 0:35:02
0:35:02
 0:23:56
0:23:56
 0:23:50
0:23:50
 0:54:01
0:54:01
 0:21:25
0:21:25
 0:53:13
0:53:13
 0:00:33
0:00:33
 0:24:40
0:24:40
 0:53:31
0:53:31
 0:15:44
0:15:44
 0:01:00
0:01:00
 0:14:56
0:14:56
 0:25:52
0:25:52
 0:18:22
0:18:22
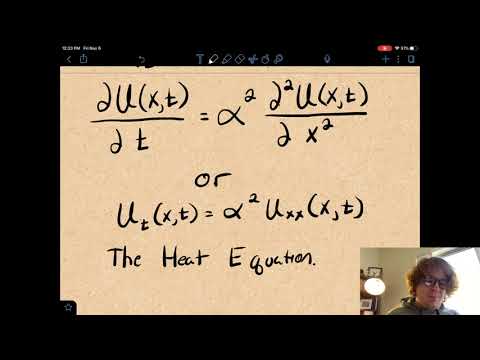 0:51:57
0:51:57
 0:19:54
0:19:54
 0:41:18
0:41:18
 0:14:22
0:14:22
 0:00:20
0:00:20
 0:19:44
0:19:44
 0:01:44
0:01:44
 0:00:31
0:00:31
 0:09:13
0:09:13