filmov
tv
Limit of (2 + h)^3 - 8 / h as h approaches 0

Показать описание
In this video, we use algebraic manipulation to find the limit as h approaches 0 of...
(2 + h)^3 - 8 / h.
If we try to find this limit as it is written, we will run into a case of 0/0, which is indeterminate.
#PreCalculus #Limits #Algebra
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
(2 + h)^3 - 8 / h.
If we try to find this limit as it is written, we will run into a case of 0/0, which is indeterminate.
#PreCalculus #Limits #Algebra
Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
Limit of (2 + h)^3 - 8 / h as h approaches 0
Evaluate the limit as x approaches 0 of ((2 + h)^3 -8)/h
Evaluate the limit as h approaches 0 of ((x+h)^3 - x^3)/h
Evaluate the limit as h approaches 0 of ( square root(9+h)-3)/h. Multiply by Conjugate
Limit of (sin(a + h) - sin(a))/h as h approaches zero (Two Solutions)
How To Find The Limit At Infinity
Elita 8: Eni prekipelo, otkrila pred svima da se Sofiji sviđa Peja - 22.10.2024.
Learn how to evaluate a limit at infinity
2 Hours Study With Me | No Music | Pomodoro 25/5 | 🪵🔥 Fire Crackling + 🌧️ Gentle Rain Sounds...
Evaluate the limit as h approaches 0 of (1/(x+h)^2 - 1/x^2)/h.
Find the Limit of (sqrt(x + h) - sqrt(x))/h as h approaches 0
BGMI Time Limit Problem fixed 🔥 #bgmi #timelimit #problem #shorts #india #hindi
How To Find a Limit using the Difference of Square Formula: ((5 + h)^2 - 25)/h as h approaches 0
Alternate Form of The Limit Definition of the Derivative - Calculus
Derivatives using limit definition - Practice problems!
Elita 8: Afera 'kofer' dobila svoj epilog, Raško vratio i Jeleni i Kačavendi kofere - 22....
How to evaluate the limit if it exists examples
Proof of a Limit Value Using Epsilon and Delta
Find a Function and x-value From Limit Definition of the Derivative
Unlock the speed limit on the HERO S8/S9
Evaluate the limit. lim_h →0 sin2 h sin3 h/h^2
Evaluate the limit using sine and cosine special limits
PreCalculus | Limit of a function (h-method)
How to set a schedule in zoom meeting with no time limit
Комментарии
 0:03:25
0:03:25
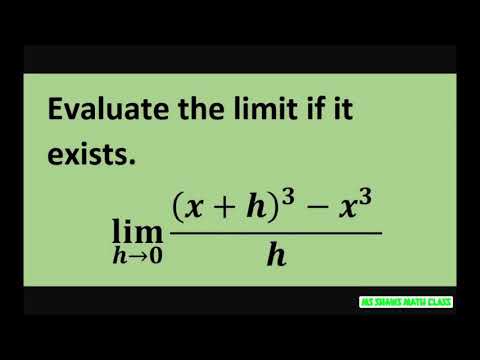 0:03:28
0:03:28
 0:04:23
0:04:23
 0:03:52
0:03:52
 0:13:14
0:13:14
 0:03:54
0:03:54
 0:01:40
0:01:40
 1:58:07
1:58:07
 0:04:56
0:04:56
 0:03:09
0:03:09
 0:00:19
0:00:19
 0:02:41
0:02:41
 0:08:10
0:08:10
 0:13:43
0:13:43
 0:02:42
0:02:42
 0:03:31
0:03:31
 0:09:17
0:09:17
 0:02:24
0:02:24
 0:00:32
0:00:32
 0:00:33
0:00:33
 0:02:06
0:02:06
 0:24:55
0:24:55
 0:03:51
0:03:51