filmov
tv
A very interesting differential equation.
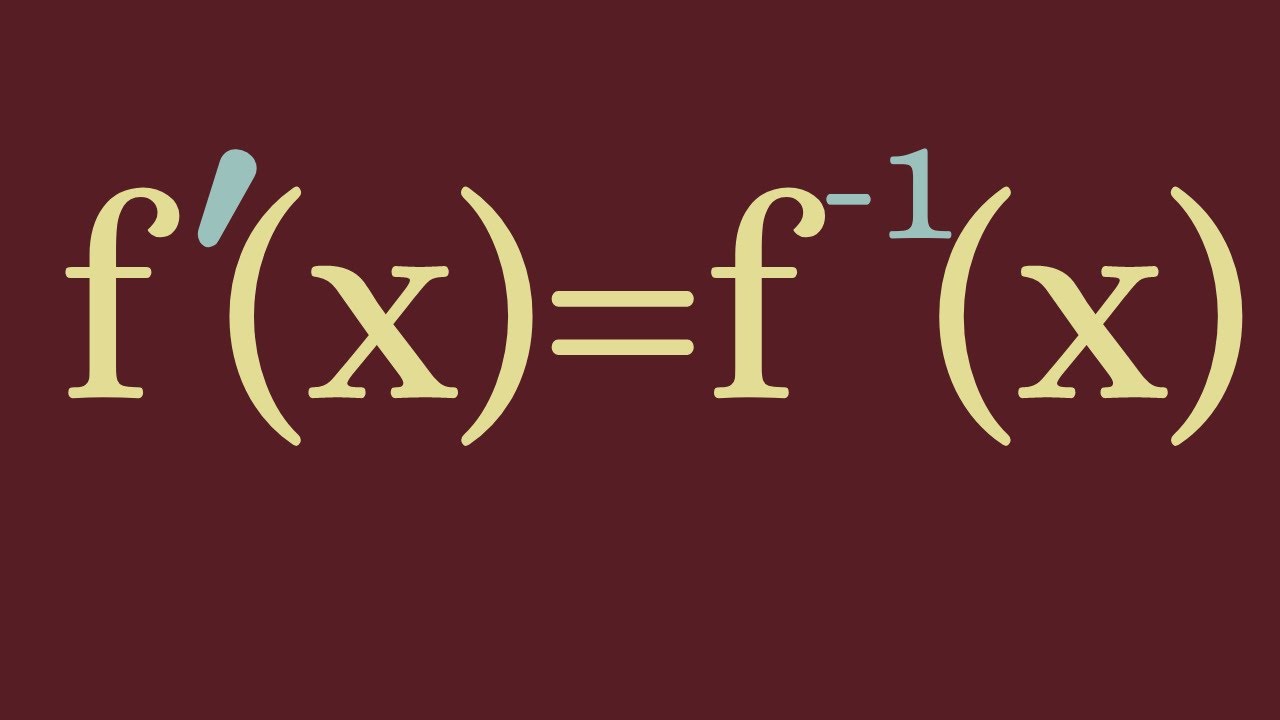
Показать описание
We present a solution to a very interesting differential equation. In particular, we find a solution to the differential equation f'(x)=f^(-1)(x). That is, we answer the question: When is the derivative of a function the same as its inverse?
Books I like:
Abstract Algebra:
Number Theory:
Calculus:
Books I like:
Abstract Algebra:
Number Theory:
Calculus:
A very interesting differential equation.
a very interesting differential equation
A very interesting differential equation
This is why you're learning differential equations
Differential equations, a tourist's guide | DE1
A deceivingly difficult differential equation
The most interesting differential equation you have seen.
a surprising differential equation
🎓 Types of Differential Equations| #MTH325
An Interesting Differential Equation | Calculus
Solving an Exact Differential Equation
Is Differential Equations a Hard Class #shorts
What are differential equations?
Differential Equations Book for Beginners
Differential equation introduction | First order differential equations | Khan Academy
A Special Differential Equation | Inspired by @blackpenredpen
a PHInominal differential equation
Differential Equations the COOL way
What is a differential equation? Applications and examples.
ODE | What is a differential equation?
Differential Equations and Dynamical Systems: Overview
How to solve ANY differential equation
If You are Thinking About Taking Differential Equations Watch This #shorts
5 simple unsolvable equations
Комментарии
 0:16:28
0:16:28
 0:21:26
0:21:26
 0:10:03
0:10:03
 0:18:36
0:18:36
 0:27:16
0:27:16
 0:16:52
0:16:52
 0:21:16
0:21:16
 0:01:26
0:01:26
 0:00:04
0:00:04
 0:10:46
0:10:46
 0:02:46
0:02:46
 0:00:21
0:00:21
 0:03:41
0:03:41
 0:00:25
0:00:25
 0:07:49
0:07:49
 0:08:20
0:08:20
 0:22:08
0:22:08
 0:05:51
0:05:51
 0:02:11
0:02:11
 0:02:23
0:02:23
 0:29:31
0:29:31
 0:05:05
0:05:05
 0:00:29
0:00:29
 0:00:50
0:00:50