filmov
tv
Integral of e^x cos(x)
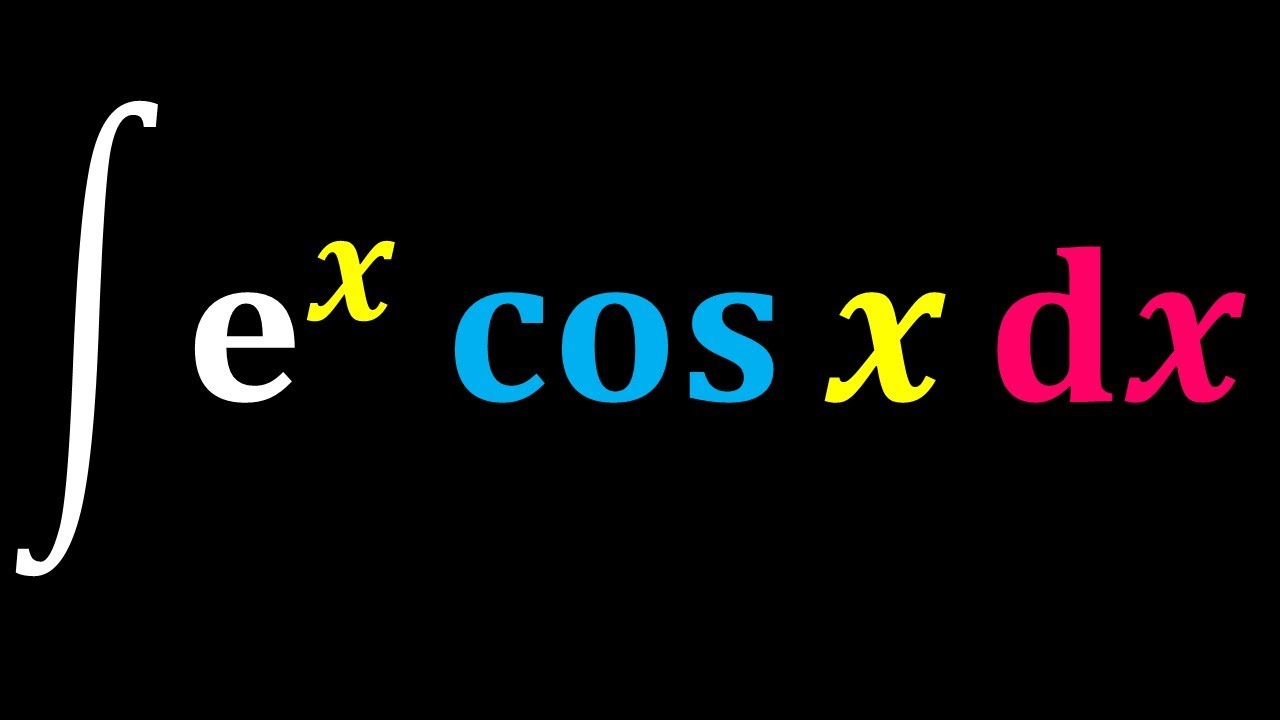
Показать описание
Tabular Integration of ∫e^x cos(x) dx:
Differentiate (D) e^x and Integrate (I) cos(x) repeatedly:
D: e^x, e^x, e^x, e^x
I: cos(x), -sin(x), -cos(x), sin(x)
Multiply diagonally and alternate signs:
(+) e^x * cos(x), (-) e^x * (-sin(x)), (+) e^x * (-cos(x)), (-) e^x * sin(x)
Add the products and their signs:
∫e^x cos(x) dx = e^x cos(x) + e^x sin(x) - e^x cos(x) - e^x sin(x) + C
Simplify the expression:
∫e^x cos(x) dx = (e^x)(cos(x) + sin(x)) + C
Remember to include a constant of integration (C) at the end.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
Differentiate (D) e^x and Integrate (I) cos(x) repeatedly:
D: e^x, e^x, e^x, e^x
I: cos(x), -sin(x), -cos(x), sin(x)
Multiply diagonally and alternate signs:
(+) e^x * cos(x), (-) e^x * (-sin(x)), (+) e^x * (-cos(x)), (-) e^x * sin(x)
Add the products and their signs:
∫e^x cos(x) dx = e^x cos(x) + e^x sin(x) - e^x cos(x) - e^x sin(x) + C
Simplify the expression:
∫e^x cos(x) dx = (e^x)(cos(x) + sin(x)) + C
Remember to include a constant of integration (C) at the end.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
0:04:43
How to integrate e^x cosx using Integration by Parts
0:07:14
Integration by parts of (e^x)(cos x)
0:03:47
Class 12th – Integral of e^x cos x dx | Integrals | Tutorials Point
0:02:47
Integration by Parts: Integral of e^x cos x dx
0:09:30
Integral e^x cos x two ways
0:04:23
Stammfunktion, Typ Phönix mit e^x und cos(x), Integralrechnung, partielle Integration
0:06:01
Integral of e^x cos(x)
0:06:13
What is an antiderivative of e^x cos x? - Week 14 - Lecture 4 - Mooculus
0:01:49
7.Finding the Derivative of e^x cos(x) Using the Product Rule | Step-by-Step Explanation
0:10:05
How to Integrate Exponential and Trigonometric Functions (e^x)(Cosx) - Sneaky Trick
0:07:03
Integración por partes de e^x cos x , que es una integral cíclica
0:03:15
Integral de e^x cos x
0:02:53
How to Integrate xcosx - Integration by Parts Worked Example
0:04:53
Integración por partes: Caso exponencial/trigonométrica
0:03:48
Integration of e^x(sin x + cos x) || Integration by parts
0:02:27
Integral of (e^x)cos(e^x) ❖ Calculus ❖ Trig Integrals
0:02:17
Integral of (e^x + cos x)/(e^x + sin x) ❖ Calculus 1
0:04:15
Integral of e^x(cos x - sin x) || Integration by parts
0:07:51
Integration by Parts: Integral of xe^(x)cos(x) dx
0:00:31
Ejercicio N°5 - ∫e^sen (x) cos(x) dx
0:01:19
How to Find the Integral of e^(sin(x))cos(x) by making a Substitution
0:08:50
Integration by Parts e^(-x) cos 2x dx example 14. LIATE
0:14:58
A fascinating holiday special: integral of e^cos(x) from 0 to pi/2
0:03:33
Integral of e^x(sin x - cos x) || Integration by parts
Комментарии