Olympiad Question! Can you Prove: (1/x + 1/y = 1/z) IF (11^x = 17^y = 187^z)? | Simple Explanation

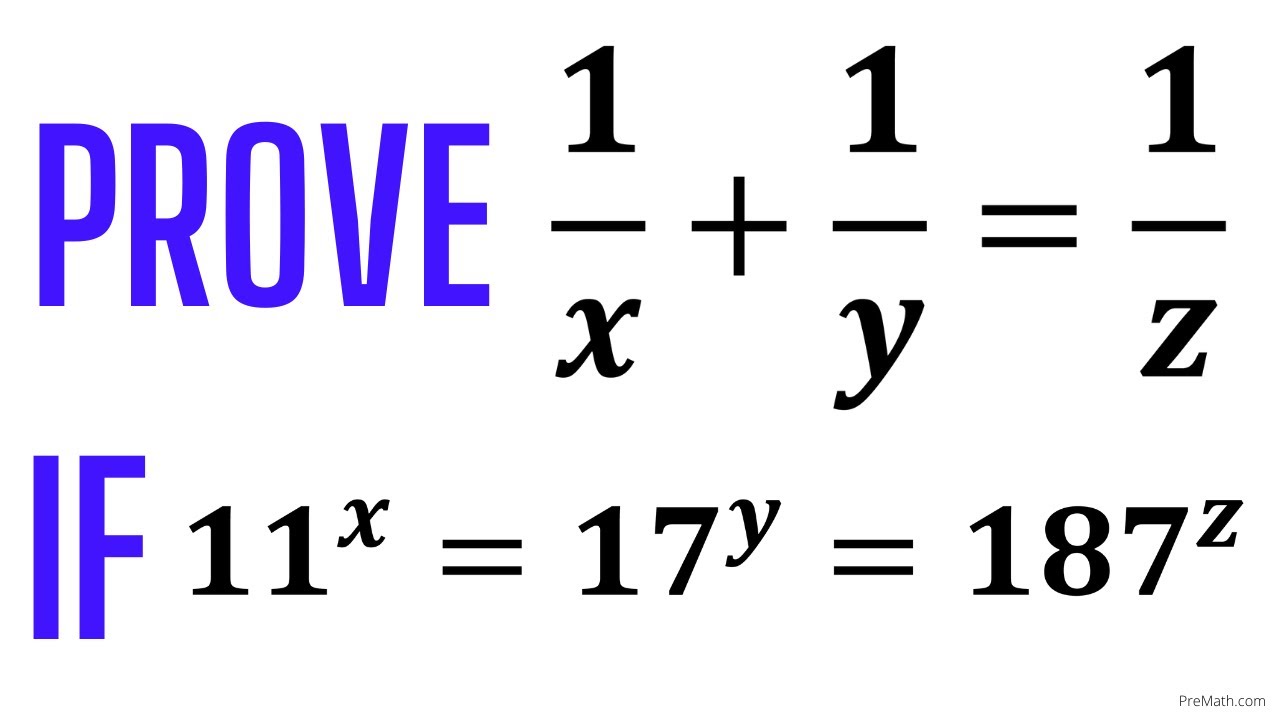
preview_player
Показать описание
  1. PreMath
  2. CBSE
  3. board
  4. exam
  5. maths
  6. Premath
Рекомендации по теме
Moscow Middle School 0:04:14

Moscow Middle School Math Olympiad Question. Can you prove this inequality in one minute?

Norway Math Olympiad 0:03:21

Norway Math Olympiad Question | You should be able to solve this!

A Nice Math 0:02:34

A Nice Math Olympiad Exponential Equation 3^x = X^9

Olympiad Question! Can 0:05:57

Olympiad Question! Can you Prove: (1/x + 1/y = 1/z) IF (11^x = 17^y = 187^z)? | Simple Explanation

Math Olympiad Question 0:01:54

Math Olympiad Question | Equation solving | You should learn this trick to pass the exam

Romania National Olympiad 0:08:54

Romania National Olympiad Question | Can you prove the sum of the three squares can't be a prim...

Luxembourg - Math 0:02:51

Luxembourg - Math Olympiad Question | You should know this trick

A Nice Olympiad 0:00:52

A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents

Find the different 0:00:11

Find the different one? #viral #quiz #trending #ytshorts #quizevolve #trendingshorts

Mexico - A 0:08:36

Mexico - A Nice Math Olympiad Exponential Problem

Prove inequality: simple 0:04:41

Prove inequality: simple trick solves it quickly | Moscow Math Olympiad question

Math Olympiad Question 0:09:54

Math Olympiad Question - Can You Spot the Trick?

Solving an IMO 0:06:40

Solving an IMO Problem in 6 Minutes!! | International Mathematical Olympiad 1979 Problem 1

Can You Prove 0:06:25

Can You Prove The Given Equation ? | Math Olympiad Exercise

Math Olympiad Question 0:15:51

Math Olympiad Question - Can You Spot the 1 Line Solution?

Cambridge University's BEST 0:13:19

Cambridge University's BEST KEPT SECRET for Solving tricky Algebra Problems

The Hardest Math 0:00:28

The Hardest Math Test

Solving the hardest 0:11:26

Solving the hardest question of a British Mathematical Olympiad

Math Olympiad Question, 0:09:31

Math Olympiad Question, Beautiful Exponential Equation. Can you solve and prove?

Math Olympiad Question 0:04:47

Math Olympiad Question | 99% don’t know how to solve it😱 You should know this Trick!!

Solving the Legendary 0:08:03

Solving the Legendary IMO Problem 6 in 8 minutes | International Mathematical Olympiad 1988

Google AI dominates 0:08:18

Google AI dominates the Math Olympiad. But there's a catch

First International Maths 0:07:50

First International Maths Olympiad Question | IMO 1959 | Proof by Absurdity or Contradiction

How to Answer 0:00:27

How to Answer Any Question on a Test

Комментарии
Автор

Just let 11 = 187 power z/x and 17 = 187 power z/y then 11 x 17 = 187 power z/x + z/y Thus z/x + z/y = 1 and finally 1/x + 1/y = 1/z Most easily solved question

Teamstudy
Автор

That was really very easy question..
I have done such questions before.

That's a very good video. Keep it up Premath.

tanmayupadhyay
Автор

Revered sir, I did I by using logarithms followed by substituting log17/log11=u, I could do it.I still follow the old methods taught in my school.Inspire of new techniques old ones always come in handy.Thanks a million GURUJI.

jaggisaram
Автор

sure can bro, thanks for sharing this multivariable problem

math
Автор

It seems very easy to me. I have solved it in 20 seconds. I have solved it orally after solving it by writing.

mustafizrahman
Автор

Excellent. It doesn't occur for a person like me to consider a fraction as exponentials to 11, 17 and 187. Extraordinary application of mind.👍👌

ramanivenkata
Автор

Logically correct.
But mathematically ?

kitchenlessindia
Автор

Super duper bumper easy question Ans I solved it mentally in few seconds....

Teamstudy
Автор

Ok, I don't have the time to watch the video for now.

lazaremoanang
Автор

187^(z) = k
(187^(z))^(1 ÷ z) = k^(1 ÷ z)
k^(1 ÷ z) = 187

theophonchana