filmov
tv
The continuous Fourier Transform of rect and sinc functions (animation)

Показать описание
The continuous Fourier transform takes an input function f(x) in the time domain and turns it into a new function, ƒ̂(x) in the frequency domain.
In the first animation, the Fourier transform (as usually defined in signal processing) is applied to the rectangular function, returning the normalized sinc function.
In the first animation, the Fourier transform (as usually defined in signal processing) is applied to the rectangular function, returning the normalized sinc function.
The continuous Fourier Transform of rect and sinc functions (animation)
Continuous Time and Discrete Time Fourier Transforms
Continuous Time Fourier Transform explained visually
Fourier Transform Equation Explained ('Best explanation of the Fourier Transform on all of YouT...
But what is the Fourier Transform? A visual introduction.
Continuous Fourier Transform
Continous Time Fourier Transform -1
Fourier Series introduction
The continuous Fourier Transform of rect and sinc functions simulation
Introduction to Fourier Transform
Coding Adventure: Sound (and the Fourier Transform)
Continuous Time Fourier Transforms | Fourier Transforms | Signals and Systems | Problem 1
Introduction to Fourier Transform CTFT/FT (Continuous Time Fourier Transform)
Continuous-time Fourier Transform
How are the Fourier Series, Fourier Transform, DTFT, DFT, FFT, LT and ZT Related?
Chapter 04 Part 1: The Continuous-Time Fourier Transform for Aperiodic Signals
Continuous Time Fourier Transform Multiplication Property
Why do we use the Fourier Transform?
Example 4.1 || Fourier Transform || Continuous Time Fourier Transform || | S&S 4.1
The Discrete Fourier Transform: Most Important Algorithm Ever?
Fourier Transform, Fourier Series, and frequency spectrum
Continuous Time Fourier Transform of a Periodic Signal
What is the difference between the Fourier Series and Fourier Transform?
Introduction to Continuous Time Fourier Transform (CTFT) In signals and system || EC Academy
Комментарии
 0:00:45
0:00:45
 0:09:24
0:09:24
 0:04:18
0:04:18
 0:06:26
0:06:26
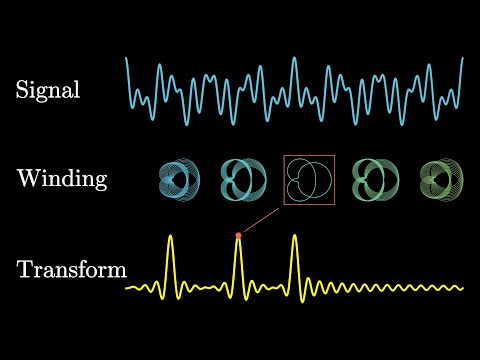 0:20:57
0:20:57
 0:17:39
0:17:39
 0:12:09
0:12:09
 0:05:12
0:05:12
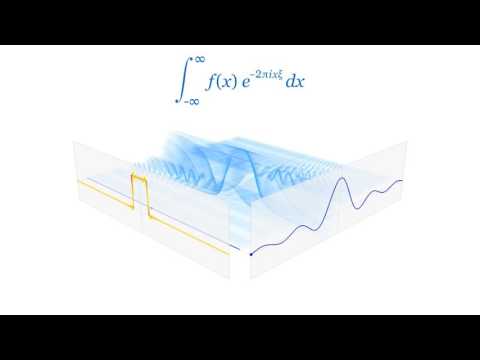 0:00:45
0:00:45
 0:06:22
0:06:22
 0:43:31
0:43:31
 0:10:24
0:10:24
 0:06:50
0:06:50
 0:08:32
0:08:32
 0:22:47
0:22:47
 0:51:12
0:51:12
 0:11:02
0:11:02
 0:00:59
0:00:59
 0:30:02
0:30:02
 0:29:24
0:29:24
 0:15:46
0:15:46
 0:01:52
0:01:52
 0:00:56
0:00:56
 0:05:09
0:05:09