filmov
tv
Sum of Binomial Coefficients
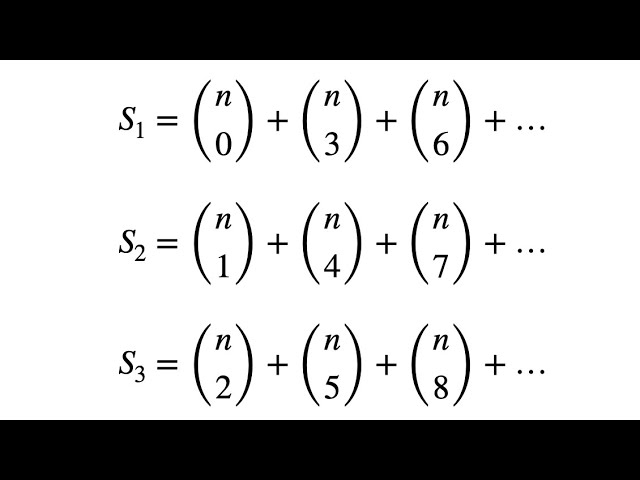
Показать описание
This exquisite problem based on the sum of binomial coefficients spaced 3 terms apart finds its resolution by leveraging a concept at the heart of the theory of complex Numbers, namely the complex cube roots of unity. How remarkable it is that a problem posed entirely in the real numbers makes use of complex numbers. But even more remarkable, and what the viewer witnesses first hand, is the mathematical interplay between the terms of the calculation that leads to the cancellation of all imaginary components present in each of the three different equations, thus yielding answers which consist purely of real numbers. So follow us on this journey as we solve a problem that serves as one of the bridges between complex numbers and sums of binomial coefficients. Not only will you see the interconnectedness of mathematical theories, but you will also have the benefit of learning some useful tools that will then be at your disposal in future instances when encountering challenging mathematical problems based on similar concepts. If you do decide to embark on this journey and watch the video from start to finish, all that is left for me to say is thank you.
Problem credit: Taken from the Book 'Higher Algebra'
Authors: Barnard and Child
Taken from Chapter 5
Chapter 5 title: Complex Numbers
Published by: Arihant Publications
Problem credit: Taken from the Book 'Higher Algebra'
Authors: Barnard and Child
Taken from Chapter 5
Chapter 5 title: Complex Numbers
Published by: Arihant Publications
 0:07:10
0:07:10
 0:02:47
0:02:47
 0:19:07
0:19:07
 0:08:27
0:08:27
 0:09:09
0:09:09
 0:02:49
0:02:49
 0:08:37
0:08:37
 0:02:17
0:02:17
 0:13:41
0:13:41
 0:12:30
0:12:30
 0:07:24
0:07:24
 0:02:46
0:02:46
 0:00:21
0:00:21
 0:12:30
0:12:30
 0:27:29
0:27:29
 0:02:57
0:02:57
 0:08:31
0:08:31
 0:00:32
0:00:32
 0:01:50
0:01:50
 0:05:47
0:05:47
 0:09:54
0:09:54
 0:05:31
0:05:31
 0:06:33
0:06:33
 0:17:39
0:17:39