filmov
tv
Sum of binomial coefficients
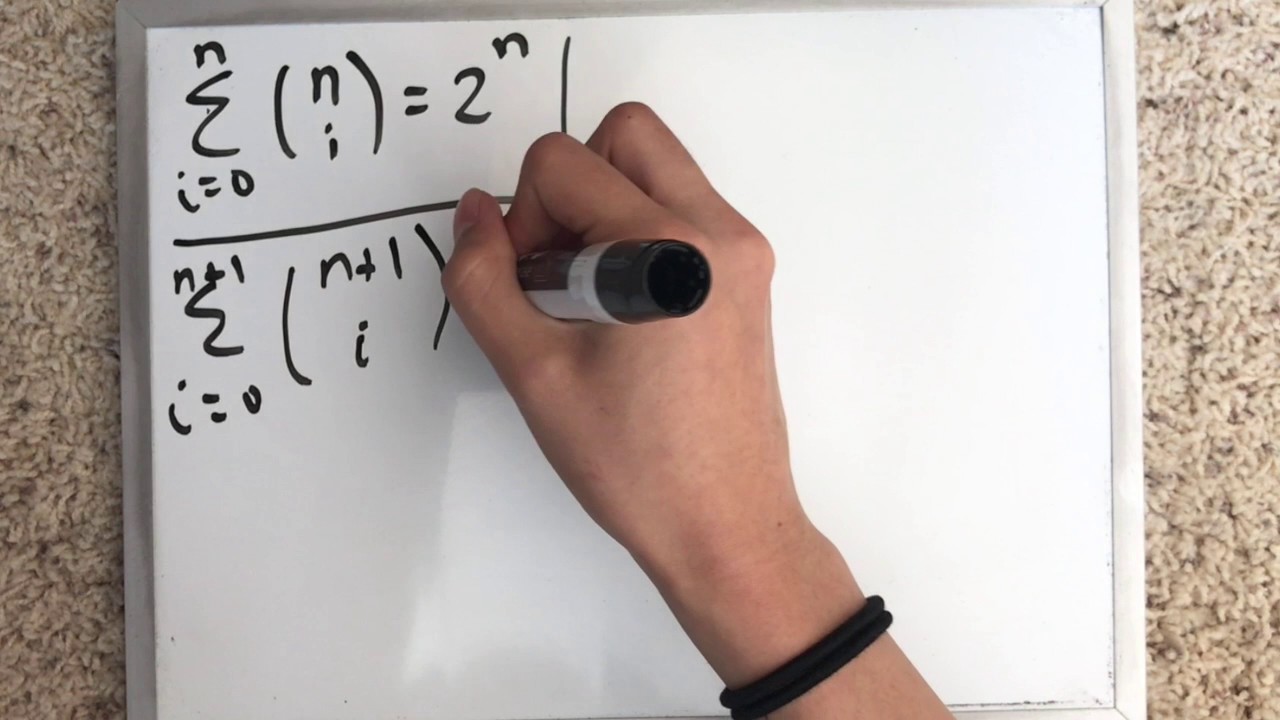
Показать описание
In this video, we are going to prove that the sum of binomial coefficients equals to 2^n.
Sum of binomial coefficients
Summing Binomial Coefficients (Exam Question)
Summing Coefficients of a Binomial Expansion
Sum of coefficients of multinomial and binomial expansion | Binomial shortcut
Sum of binomial coefficients | An elegant proof
Something special with these binomial coefficient sums
How To Evaluate Binomial Coefficients
Sum of Binomial Coefficients
Summation of Binomial Coefficients- Part 1 | Maths Class 11
Binomial Sums and Beyond
Sum of Binomial Coefficients | To Crack JEE Main & JEE Advanced Problems | #jee #sameerchincholi...
Sum of Binomial Coefficients
Binomial Coefficients: Examples Part 1
Deriving sum of A.P binomial coefficients
Even Binomial Coefficient Sum
Sum of binomial coefficients, odd binomial coefficients, even binomial coefficients
Binomial Coefficients Bible with Strategy to Prove Many Identities Anil Kumar Lesson
SUM OF BINOMIAL COEFFICIENTS
Sum of coefficients of binomial expansion|| sum of all coefficients in binomial expansion
Solve Binomial Series in 5 Seconds | IIT JEE Short Cuts & Tricks | JEE Main 2022 | MathonGo
Prove that Sum(n choose r) = 2^n
Binomial series: Lecture 5: Sum of all the coefficients in the expansion
Sum of Polynomial Coefficients Challenge
Find the coefficient of x^5 in the binomial expansion of (2x-8)^8
Комментарии
 0:02:47
0:02:47
 0:08:27
0:08:27
 0:02:17
0:02:17
 0:07:24
0:07:24
 0:07:10
0:07:10
 0:08:31
0:08:31
 0:08:37
0:08:37
 0:19:07
0:19:07
 0:13:41
0:13:41
 0:12:30
0:12:30
 0:12:30
0:12:30
 0:09:09
0:09:09
 0:08:38
0:08:38
 0:00:21
0:00:21
 0:02:46
0:02:46
 0:06:33
0:06:33
 0:27:29
0:27:29
 0:05:31
0:05:31
 0:02:49
0:02:49
 0:03:52
0:03:52
 0:01:40
0:01:40
 0:05:47
0:05:47
 0:00:37
0:00:37
 0:03:50
0:03:50