filmov
tv
Subgroups of (R, +) are Dense or Cyclic
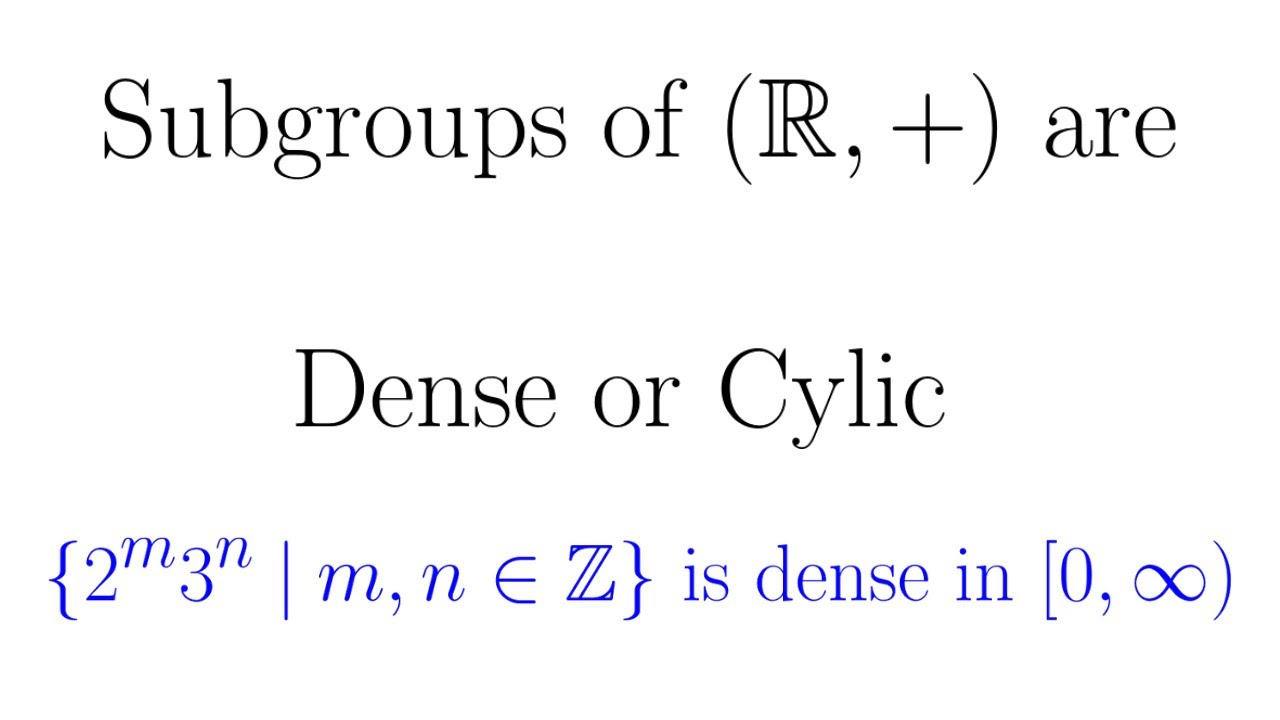
Показать описание
I prove all subgroups of additive group of real numbers are either cyclic or dense. Then, we use that to show the set of rationals of the form 2^m 3^n is dense in [0, infty).
Subgroups of (R, +) are Dense or Cyclic
Mark Sapir: On subgroups of the R. Thompson group F
A Brief Introduction to Normal Subgroups of a Group in Abstract Algebra
Subgroups of Group of Integers with Addition
Creating Subgroups of Data in R
Subgroups of Real Numbers. How do they look like?
Calculate Mean Square for Subgroups in R
M1106 - Analysis IV - Chapter 1 - Appendix A - On additive subgroups of R
QUESTION ON SUBGROUPS OF C* AND R* || IIT JAM || GATE || NET || TIFR
Collin Bleak - On the complexity of elementary amenable subgroups of R. Thompson's group F
Abstract Algebra Subgroups Cyclic Subgroups
Subgroups of the additive group of integers (Artin 2.3) | Abstract Algebra 23
Visual Group Theory, Lecture 3.1: Subgroups
Overview of Subgroup Analysis
Subgroups of a cyclic group
Abstract Algebra Lectures Part 2: Generators, Order, Cyclic Subgroups
4 subgroups
[Deprecated] Group Theory Lecture 2.2 Examples of Subgroups
GT7. The Commutator Subgroup
Examples of Subgroups
NIP approximate subgroups
Subgroups: definition and examples
Subgroups
Subgroups
Комментарии
 0:17:22
0:17:22
 0:55:59
0:55:59
 0:04:03
0:04:03
 0:07:00
0:07:00
 0:05:32
0:05:32
 0:10:18
0:10:18
 0:01:36
0:01:36
 0:19:06
0:19:06
 0:10:08
0:10:08
 1:15:32
1:15:32
 0:05:47
0:05:47
 0:29:47
0:29:47
 0:13:43
0:13:43
 0:05:52
0:05:52
 0:22:21
0:22:21
 0:16:20
0:16:20
 0:27:48
0:27:48
![[Deprecated] Group Theory](https://i.ytimg.com/vi/q_wU_8qKCgQ/hqdefault.jpg) 0:17:32
0:17:32
 0:15:21
0:15:21
 0:09:11
0:09:11
 0:59:09
0:59:09
 0:16:12
0:16:12
 0:19:00
0:19:00
 0:06:34
0:06:34