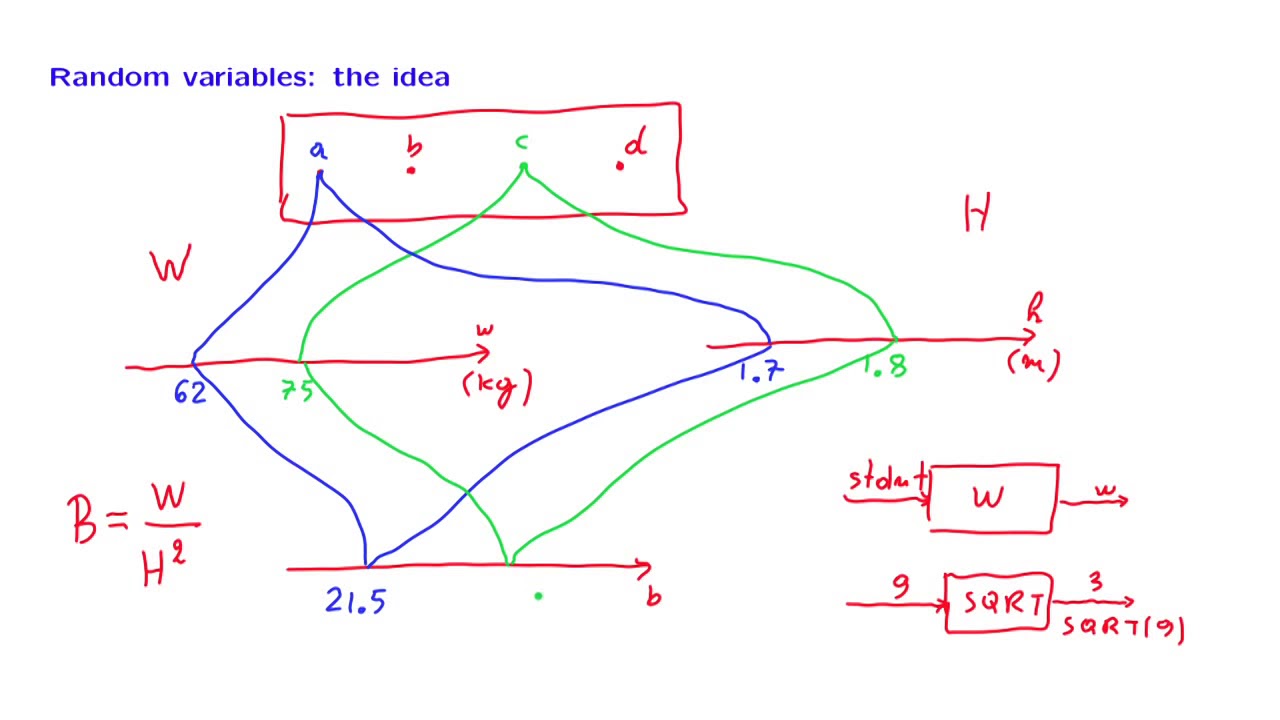
L05.2 Definition of Random Variables

MIT RES.6-012 Introduction to Probability, Spring 2018
Instructor: John Tsitsiklis

License: Creative Commons BY-NC-SA

[adnanmohamed]

I've learned about random variables from more than 3 resources but this one is special in the way of clearly explaining the concept (intuitively and mathematically)!

[sudn]

I will never forget this again in my life!

[BoZhaoengineering]

The Random variables rises so naturally that I use it forgetting about the derivation from the sample space .

[iranjackheelson]

5:58 did he mean 1 to 10? because I don't see what value would be associated w/ 0th toss

[kaushiknarayanan.c]

That's a crisp explanation about random variables!!

[marikoueno]

Thank you, sir. I really appreciate your lectures. Awsome.

[dalisabe]

How this jumble mumble explanation is different from the algebraic definition of a variable x taking on the value of a or b? How is the random variable different from the notation g(x) or f(x) or p(x) meaning that x——->f(x) that maps x value to the f value? Of course, we know that a function is just a machine that takes in an input value and spits out an output value, or simply assigns some value corresponding to every x value in the domain of the function.

Why this redundancy of randomness when it is already built into the definition of a variable? A variable is something that takes on different values opposed to a constant whether the assignment is done by deliberate selection or random chance. The idea of randomness in statistics is intimately tied to probability and chances, which is understandable, but it doesn’t call for creating weird capital letter notation just to say that the variable is random! I still don’t get it, and all those who are so impressed by the presented explanation, I would like to hear their own understanding of it.

[pradeepkumartarei]

The square root of 9 corresponds to both +3 and -3, where 9 is considered as an input and both +3 and -3 are considered as outputs. Since as per the property of a "Function", a (permissible) input can't have 2 (permissible) outputs, hence I believe the example of "SQRT" as a function is not apt here.

[duartesilva]

I don't agree with his last point. Var(X) is a function on r.v. X and, unless you are in Bayesian Statistics, it's not a random variable.

[Daniel-xaogjeyh]

MIT is a joke, these things are thought in early high school in Eastern Europe