filmov
tv
What is a Random Variable?

Показать описание
Explains what a Random Variable is, using two examples, and also discusses the associated probability density function (pdf), and how it is modelled in practice.
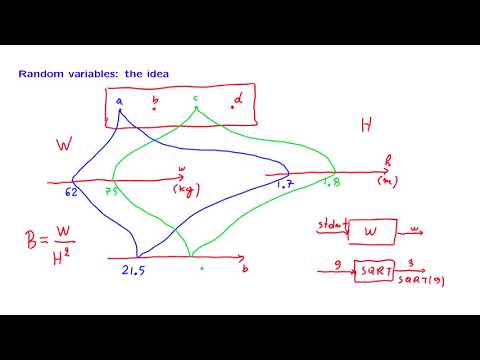
Just one note to clarify the modelling Assumptions discussed in the video: Actually there are two parts to the assumptions being made. The first, is that there are three types of people who travel on trains: those who always use WiFi when travelling on a train, those who never use WiFi when travelling on a train, and those who use it on half of the trips they make (with a random selection as to which trips they use it on). Of course this is a simplification of reality, but that is what you need to do in order to build statistical models of reasonable/practical computational size. The second part of the assumption is that each train carriage will always contain two of the first type of people, one of the second type of people, and two of the third type of people. So, depending on what the two "third type people" have chosen to do, there will either be 2 people using WiFi (if both of the "third type" people have chosen not to use WiFi on that trip), 3 people using WiFi (if only one of the "third type" people has chosen to use WiFi on that trip), or 4 people using WiFi (if both of the "third type" people have chosen to use WiFi on that trip).
* And I should point out that I must have had a brief brain fade at the 4:53 mark in the video where I wrote X's instead of Y's. In other words, the probabilities should be written P(Y=0)=0, P(Y=1)=0, etc, instead of P(X=0)=0, P(X=1)=0, ...
Just one note to clarify the modelling Assumptions discussed in the video: Actually there are two parts to the assumptions being made. The first, is that there are three types of people who travel on trains: those who always use WiFi when travelling on a train, those who never use WiFi when travelling on a train, and those who use it on half of the trips they make (with a random selection as to which trips they use it on). Of course this is a simplification of reality, but that is what you need to do in order to build statistical models of reasonable/practical computational size. The second part of the assumption is that each train carriage will always contain two of the first type of people, one of the second type of people, and two of the third type of people. So, depending on what the two "third type people" have chosen to do, there will either be 2 people using WiFi (if both of the "third type" people have chosen not to use WiFi on that trip), 3 people using WiFi (if only one of the "third type" people has chosen to use WiFi on that trip), or 4 people using WiFi (if both of the "third type" people have chosen to use WiFi on that trip).
* And I should point out that I must have had a brief brain fade at the 4:53 mark in the video where I wrote X's instead of Y's. In other words, the probabilities should be written P(Y=0)=0, P(Y=1)=0, etc, instead of P(X=0)=0, P(X=1)=0, ...
Комментарии
 0:05:32
0:05:32
 0:04:39
0:04:39
 0:11:58
0:11:58
 0:09:14
0:09:14
 0:11:56
0:11:56
 0:02:10
0:02:10
 0:08:41
0:08:41
 0:10:03
0:10:03
 0:02:25
0:02:25
 0:29:54
0:29:54
 0:02:19
0:02:19
 0:08:57
0:08:57
 0:16:23
0:16:23
 0:11:29
0:11:29
 0:07:02
0:07:02
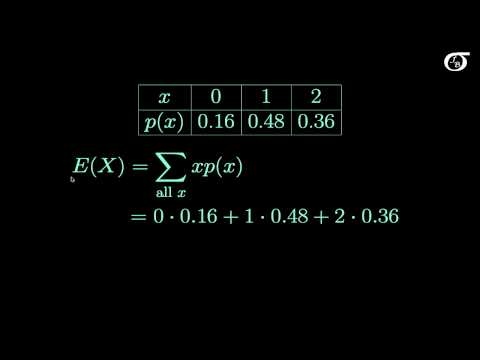 0:07:57
0:07:57
 0:14:11
0:14:11
 0:07:32
0:07:32
 0:06:46
0:06:46
 0:18:08
0:18:08
 0:05:35
0:05:35
 0:03:52
0:03:52
 0:21:51
0:21:51
 0:07:31
0:07:31