filmov
tv
Differential Equations: Population Growth: Logistic Equation: Example 2

Показать описание
In this video I prove that the growth rate in a population, assuming it uses the logistic model, is fastest at half the carrying capacity. I prove this using the first derivative test but apply it to the 1st and 2nd derivatives of the population function. In my last video I graphically showed that in fact the population appears to be growing fastest at about the half way mark, but in this video I prove it definitely. This is a very good video to understand how population sizes increase so make sure to watch this video!
Related Videos:
------------------------------------------------------
Related Videos:
------------------------------------------------------
The Logistic Growth Differential Equation
Logistic Growth Function and Differential Equations
Solving the logistic differential equation part 1 | Khan Academy
Logistic Differential Equation (general solution)
The Logistic Differential Equation for Population Growth: General Solution
Differential Equations: Population Growth: Logistic Equation
Modelling Population Growth: The Logistic Equation - Differential Equations
Worked example: Logistic model word problem | Differential equations | AP Calculus BC | Khan Academy
Introduction to Population Models and Logistic Equation (Differential Equations 31)
Logistic growth model of a population (KristaKingMath)
Ex: Logistic Growth Differential Equation
ODE | Population models
The Logistic Equation and Models for Population - Example 1, part 1
Exponential Growth and Decay Calculus, Relative Growth Rate, Differential Equations, Word Problems
Calculus BC – 7.9 Logistic Models with Differential Equations
Differential Equations: Population Growth: Logistic Equation: Example 5
Logistic differential equation intuition | First order differential equations | Khan Academy
Differential Equations: Population Growth: Logistic Equation: Example 1
The Logistic Equation
Differential Equations: Population Growth: Logistic Equation: Example 2
Modeling population with simple differential equation | Khan Academy
ODE | The logistic population model
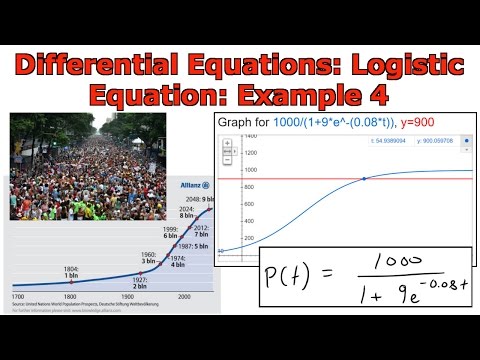
Differential Equations: Population Growth: Logistic Equation: Example 4
Logistic growth: finding equilibrium solutions
Комментарии
 0:08:54
0:08:54
 0:43:07
0:43:07
 0:13:38
0:13:38
 0:10:52
0:10:52
 0:15:05
0:15:05
 0:11:40
0:11:40
 0:09:52
0:09:52
 0:08:47
0:08:47
 1:04:39
1:04:39
 0:06:26
0:06:26
 0:07:11
0:07:11
 0:06:02
0:06:02
 0:07:04
0:07:04
 0:13:02
0:13:02
 0:16:28
0:16:28
 0:20:28
0:20:28
 0:10:48
0:10:48
 0:12:25
0:12:25
 0:13:27
0:13:27
 0:18:11
0:18:11
 0:07:40
0:07:40
 0:04:48
0:04:48
 0:13:10
0:13:10
 0:04:10
0:04:10