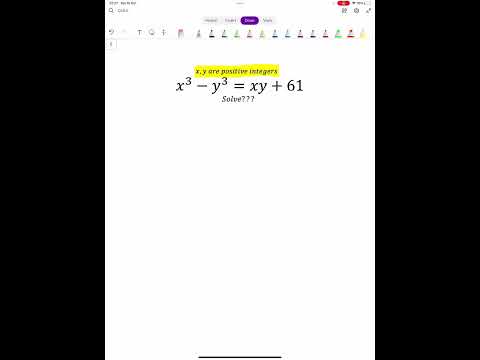
#shorts The Russian number theory puzzle - Math problem of the day

Another video in the new short series - Math of the Day!

Give us your answers in the comments and feel free to discuss!

Press the bell icon to get new exciting math problems every day!

#maths #mathoftheday #math #mathsfun #russian #mathematics #mathstricks #mathjee #mathtricks #mathskills #ndamaths #ndamathematics #bankmath #mathsisfun
Ramanujan #viralmathproblem #viral #viralvideo #viralshorts #mathpuzzles

[mfn]

Since 2^n is always even that means n^2 needs to be odd for it to end in 5. 2^ an odd number will always give either the last digit as a 2 or an 8, that means that n^2 must end in either a 3 or a seven for 2^n + n^2 to end in a 5. An odd number squared will always give depending on the last digit, 1, 5 or 9, meaning it doesn’t work.

[masaru_mf]

I think nope.
Let n be some number n = 10k+5 = 5(2k+1). As you can see, we just proved if a natural ends with 5 it’s multiple of 5, whereas if this isn’t true, then our number can’t end with 5.
Let’s introduce in our expression some number 5k.
2^(5k)+(5k)^2 = n = 5k
(2^(5k)+(5k)^2)/5 = k
(2^(5k))/5 + 5k^2 = k
Since (2^(5k))/5 is an irreducible rational and 5k^2 is integer, that expression can’t be integer, so we conclude that if n is ends with 5, then the result of 2^n+n^2 can’t be a multiple of 5 and therefore, it can’t end with 5 for any n natural.