filmov
tv
a very TRICKY double absolute value equation
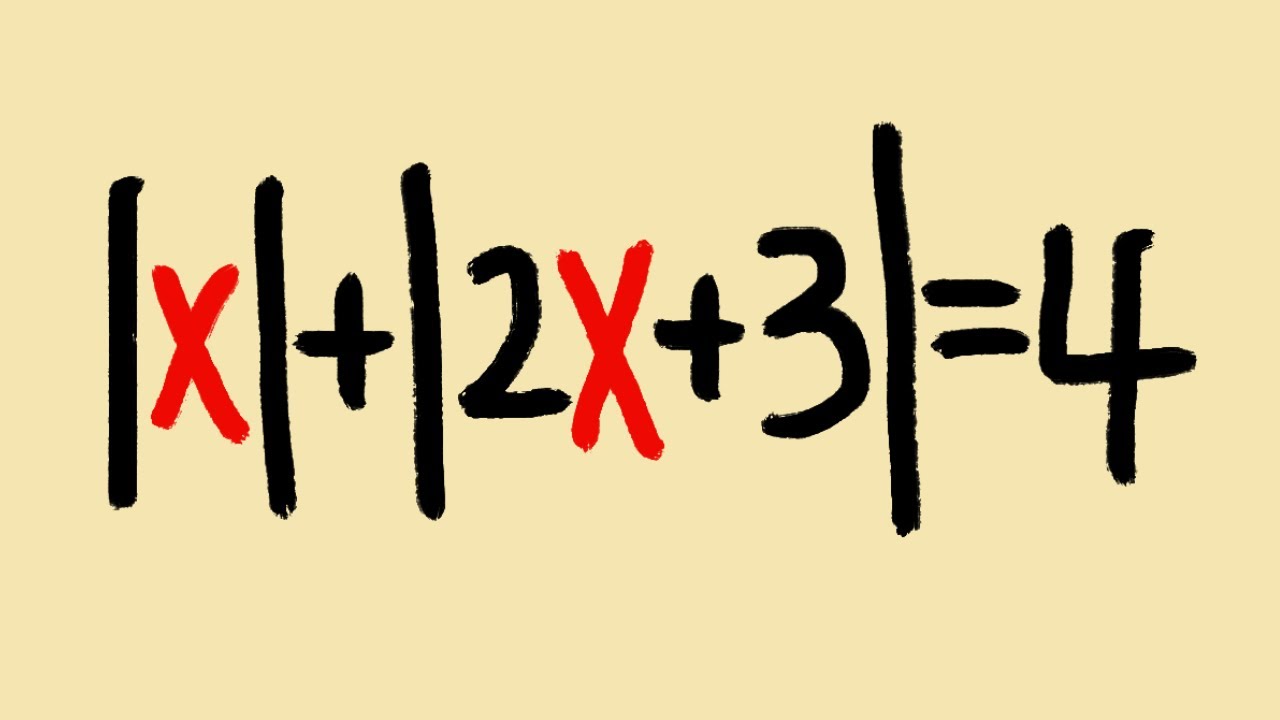
Показать описание
This equation has two absolute values. It seems like it will give use 4 answers at first but two of them are actually extraneous! So we must be careful when we solve this kinda double absolute value equation. Be sure to try the two practice problems at the end of the video.
Use "WELCOME10" for 10% off
-----------------------------
If you find my channel helpful and would like to support it 💪, then you can
-----------------------------
"Just Algebra" (by blackpenredpen) is dedicated to helping middle school, high school, and community college students who need to learn algebra. Topics include how to solve various equations (linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more), factoring techniques, word problems, functions, graphs, Pythagorean Theorem, and more. We will also cover standardized test problems such as the SAT. Free feel to leave your questions in the comment!
-----------------------------
#justalgebra
Use "WELCOME10" for 10% off
-----------------------------
If you find my channel helpful and would like to support it 💪, then you can
-----------------------------
"Just Algebra" (by blackpenredpen) is dedicated to helping middle school, high school, and community college students who need to learn algebra. Topics include how to solve various equations (linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more), factoring techniques, word problems, functions, graphs, Pythagorean Theorem, and more. We will also cover standardized test problems such as the SAT. Free feel to leave your questions in the comment!
-----------------------------
#justalgebra
Комментарии
 0:04:59
0:04:59
 0:02:56
0:02:56
 0:06:50
0:06:50
![[March SAT Math]](https://i.ytimg.com/vi/l-BH7YECeSk/hqdefault.jpg) 0:01:00
0:01:00
 0:40:33
0:40:33
 0:09:09
0:09:09
 0:07:26
0:07:26
 0:09:42
0:09:42
 0:12:39
0:12:39
 0:34:46
0:34:46
 0:14:21
0:14:21
 0:05:22
0:05:22
 0:00:40
0:00:40
 0:03:09
0:03:09
 0:56:10
0:56:10
 0:06:03
0:06:03
 0:20:53
0:20:53
 0:12:04
0:12:04
 0:00:16
0:00:16
 1:26:24
1:26:24
 0:08:01
0:08:01
 0:01:54
0:01:54
 0:17:07
0:17:07
 0:00:35
0:00:35