Prove that 17n^3 + 103n is Divisible by 6 using Mathematical Induction

preview_player
Показать описание
Prove that 17n^3 + 103n is Divisible by 6 using Mathematical Induction

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus Integration Insanity

Differential Equations Course

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)
  1. The Math Sorcerer
  2. Prove that 17n^3 103n is Divisible by 6 using Mathematical Induction
Рекомендации по теме
Prove that 17n^3 0:13:53

Prove that 17n^3 + 103n is Divisible by 6 using Mathematical Induction

Using Mathematical Induction 0:06:17

Using Mathematical Induction to Prove 2^(3n) - 3^n is divisible by 5

17n^3+103n é divisível 0:11:11

17n^3+103n é divisível por 6 para qualquer natural? | Princípio da Indução Finita

Prove that n^3 0:12:23

Prove that n^3 + 2n is divisible by 3 using Mathematical Induction

Induction - Two 0:12:59

Induction - Two divisibility problems

How a^3 - 0:02:01

How a^3 - a is divisible by 6 ?

103N. Carrier Movement 0:28:34

103N. Carrier Movement in Semiconductors, Drift and Diffusion

Discrete Mathematics - 0:53:18

Discrete Mathematics - Induction & Induction Proofs

Mathematical Induction Proof: 0:14:43

Mathematical Induction Proof: 5^(2n + 1) + 2^(2n + 1) is Divisible by 7

a^2 - 1 0:03:20

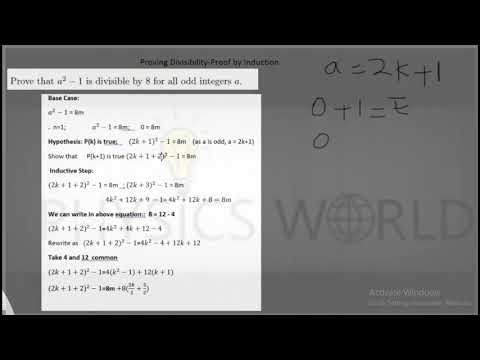
a^2 - 1 is divisible by 8 || Odd integer || Proving Divisibility || Proof by Induction

If you don't 0:04:36

If you don't do this you CAN'T get better at math

Proof: The Product 0:05:15

Proof: The Product of Two Consecutive Integers is Even

Mathematical Induction Proof: 0:09:07

Mathematical Induction Proof: n^2 - 1 is divisible by 8 for all odd positive integers

Proof of the 0:03:21

Proof of the Right Cancellation Law in a Group

Real numbers_Cbse_Class 10_ 0:10:32

Real numbers_Cbse_Class 10_ n³ - n divisible by 6

Prove by Mathematical 0:15:08

Prove by Mathematical induction |1/1.2.3+1/2.3.4+1/3.4.5+.. +1/n(n+1)(n+2)= n(n+3)/4(n+1)(n+2)

@QUANDO UM NÚMERO 0:05:34

@QUANDO UM NÚMERO É DIVISÍVEL POR 12 ? @MATFUZNAV22

7.2 - Extraneous 0:13:39

7.2 - Extraneous Roots and Applications

1-Números Irracionais 0:15:06

1-Números Irracionais

Tutorial 10 hints 0:49:00

Tutorial 10 hints

Комментарии
Автор

Great video. I can't imagine the headache I would have had if you hadn't told me that the product of two consecutive integers is even.
Great example of strong induction, too. I was fuzzy on the whole thing.

alanreeves
Автор

9:04 This is a perfect example for what I'm struggling with when I'm doing my assignments. I never know when I have to prove such small things or when I can expect them to be taken for granted. The problem is that my professors sometimes prove such things and sometimes they just state them and use them, so I'm always worried that if I don't prove it, I will lose points. On the other hand, it would seem a bit much to have to prove literally everything. How would you do it?

wilhufftarkin
Автор

This comment is related to determinants

Today, I thought I found something new by doing the homework of matrices that my teacher gave . Taking out there adjoints and inverses directly I sooner came to a 2 questions matrix with 0 in a triangular form one upper left other bottom left. Surprisingly both of the pos. of the matrices came same . So I did more questions regarding 0 in matrices
Then hour later I found that it's a theorem that already existed but not explained by my teacher . The ch is finished in my school.

crtcs